Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
3.3cm
6.7cm
4.9cm
2.6cm
The correct Answer is:C
To find the amplitude of simple harmonic motion of a point on the string located at x=1.8cm, we will follow these steps:
Step 1: Write down the equations of the waves
The equations of the two waves are given as:
Y1=6cmsin(5rad/cmx−4rad/st)
Y2=6cmsin(5rad/cmx+4rad/st)
Step 2: Find the resultant wave equation
The resultant wave Y due to the superposition of Y1 and Y2 can be expressed as:
Y=Y1+Y2
Using the trigonometric identity for the sum of sines:
sinA+sinB=2sin(A+B2)cos(A−B2)
we can rewrite Y:
Y=6sin(5x−4t)+6sin(5x+4t)=12sin(5x)cos(4t)
Step 3: Identify the amplitude
From the resultant wave equation Y=12sin(5x)cos(4t), we see that the amplitude A is given by:
A(x)=12sin(5x)
Step 4: Calculate the amplitude at x=1.8cm
Substituting x=1.8cm into the amplitude equation:
A(1.8)=12sin(5×1.8)
Calculating 5×1.8:
5×1.8=9rad
Now, we find sin(9):
A(1.8)=12sin(9)
Using a calculator or sine table, we find:
sin(9rad)≈0.412
Thus,
A(1.8)≈12×0.412≈4.944cm
Step 5: Round to significant figures
Rounding 4.944cm gives approximately 4.9cm.
Final Answer
The amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm is approximately:
4.9cm
The equations of the two waves are given as:
Y1=6cmsin(5rad/cmx−4rad/st)
Y2=6cmsin(5rad/cmx+4rad/st)
The resultant wave Y due to the superposition of Y1 and Y2 can be expressed as:
Y=Y1+Y2
Using the trigonometric identity for the sum of sines:
sinA+sinB=2sin(A+B2)cos(A−B2)
we can rewrite Y:
Y=6sin(5x−4t)+6sin(5x+4t)=12sin(5x)cos(4t)
From the resultant wave equation Y=12sin(5x)cos(4t), we see that the amplitude A is given by:
A(x)=12sin(5x)
Substituting x=1.8cm into the amplitude equation:
A(1.8)=12sin(5×1.8)
Calculating 5×1.8:
5×1.8=9rad
Now, we find sin(9):
A(1.8)=12sin(9)
Using a calculator or sine table, we find:
sin(9rad)≈0.412
Thus,
A(1.8)≈12×0.412≈4.944cm
Rounding 4.944cm gives approximately 4.9cm.
The amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm is approximately:
4.9cm
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer
9 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct Answer Type
56 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described as
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
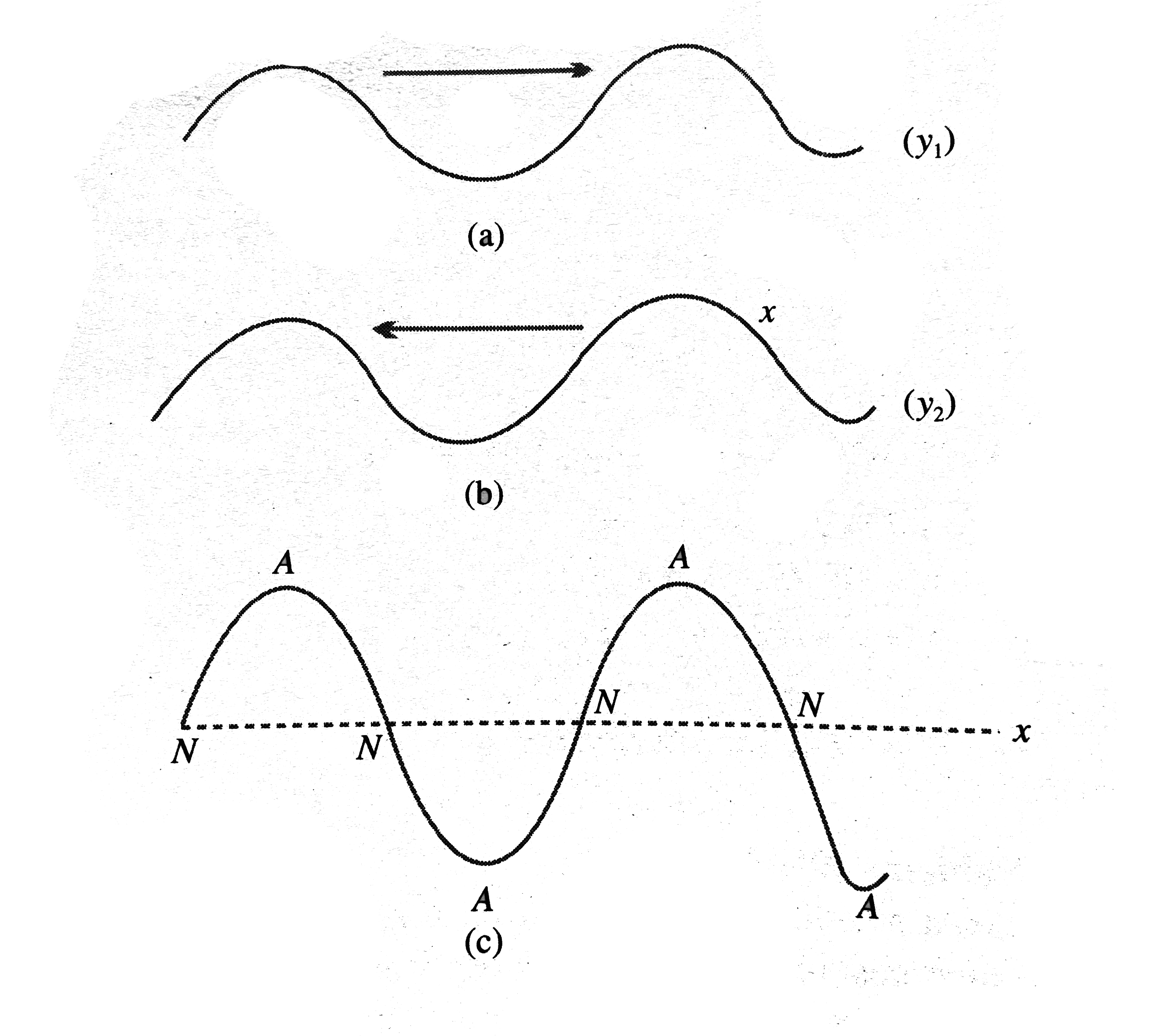
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string named as A
View Solution
Knowledge Check
The equation of a wave travelling in a string can be written as y=3cosπ(10t−x). Its wavelength is
A100 cmB2 cmC5 cmDnone of the above
In a stationary wave along a string the strain is
View SolutionA standing wave arises on a string when two waves of equal amplitude , frequency and wavelength travelling in opposite superimose. If the frequency of oscillation of the standing waves
View SolutionA standing wave is maintained in a homogeneous string of cross - sectional area a and density p . It is formed at y\he superpositions given of two waves travelling in opposite directions given by the equations
View SolutionA transverse wave is travelling on a string. The equation of the wave
View SolutionTwo wave pulses travel in opposite directions on a string and approch each other. The shape of the one pulse is same with respect to the other
View SolutionTwo waves of equal frequency f and velocity v travel in opposite directions along the same path. The waves have amplitudes A and 3A . Then:
View SolutionAssertion: Stationary waves are so called because particles are at rest in stationary waves.
Reason: They are formed by the superposition of two identical waves travelling in opposite directions.
View Solution
