Consider a uniform U-tube with a diaphragm at the bottom and filled with a liquid to different heights in each limb as shown in Fig. Now imagine that the diaphragm is punctured so that the liquid flows from left to right. (a) Show that the application of Bernoulli's particle to points (1) and Diaphragm (2) leads to a constradiction. (b) Explain why Bernoulli's principle is not applicabe here
To solve the problem step by step, we will analyze the situation using Bernoulli's principle and understand why it leads to a contradiction in this scenario.
Step 1: Understanding the Setup
We have a U-tube with a diaphragm at the bottom, filled with liquid to different heights in each limb. When the diaphragm is punctured, the liquid starts flowing from the left limb to the right limb.
Hint: Visualize the U-tube and the liquid levels in both limbs before and after the diaphragm is punctured.
Step 2: Applying Bernoulli's Equation
Bernoulli's equation states that for an incompressible, non-viscous fluid flowing in a streamline, the following holds:
P+12ρv2+ρgh=constant
Where:
- P = pressure
- ρ = density of the fluid
- v = velocity of the fluid
- g = acceleration due to gravity
- h = height above a reference level
We will apply Bernoulli's equation to two points: point (1) in the left limb and point (2) at the diaphragm.
Hint: Identify the parameters (height, velocity, and pressure) at points (1) and (2) to apply Bernoulli's equation.
Step 3: Analyzing Point (1) and Diaphragm (2)
- At point (1), the liquid is at a height h1 and has some pressure P1.
- At the diaphragm (point 2), the height is lower (let's say h2) and the pressure is P2.
Using Bernoulli's equation:
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2
Hint: Consider the implications of the heights and the velocities at these points.
Step 4: Contradiction in Velocities
If the diaphragm is punctured, the liquid will start flowing. According to Bernoulli's principle, the velocity of the fluid should increase as it moves from point (1) to point (2). However, since the liquid is flowing from left to right, the velocities at points (1) and (2) cannot be equal, leading to a contradiction.
Hint: Think about how the flow changes as the liquid moves from one point to another.
Step 5: Explanation of Non-applicability of Bernoulli's Principle
Bernoulli's principle assumes steady flow and incompressible fluid. However, in this scenario, the flow is unsteady due to the puncture in the diaphragm, and the fluid is not moving in a streamline manner. The flow is also affected by the changes in height and pressure, which do not satisfy the conditions required for Bernoulli's equation to hold.
Hint: Reflect on the assumptions of Bernoulli's equation and how they apply to this situation.
Conclusion
In conclusion, the application of Bernoulli's equation to the points in the U-tube leads to a contradiction due to the unsteady flow condition after the diaphragm is punctured. Therefore, Bernoulli's principle is not applicable in this case.
We have a U-tube with a diaphragm at the bottom, filled with liquid to different heights in each limb. When the diaphragm is punctured, the liquid starts flowing from the left limb to the right limb.
Bernoulli's equation states that for an incompressible, non-viscous fluid flowing in a streamline, the following holds:
- P = pressure
- ρ = density of the fluid
- v = velocity of the fluid
- g = acceleration due to gravity
- h = height above a reference level
- At point (1), the liquid is at a height h1 and has some pressure P1.
- At the diaphragm (point 2), the height is lower (let's say h2) and the pressure is P2.
If the diaphragm is punctured, the liquid will start flowing. According to Bernoulli's principle, the velocity of the fluid should increase as it moves from point (1) to point (2). However, since the liquid is flowing from left to right, the velocities at points (1) and (2) cannot be equal, leading to a contradiction.
Bernoulli's principle assumes steady flow and incompressible fluid. However, in this scenario, the flow is unsteady due to the puncture in the diaphragm, and the fluid is not moving in a streamline manner. The flow is also affected by the changes in height and pressure, which do not satisfy the conditions required for Bernoulli's equation to hold.
In conclusion, the application of Bernoulli's equation to the points in the U-tube leads to a contradiction due to the unsteady flow condition after the diaphragm is punctured. Therefore, Bernoulli's principle is not applicable in this case.
Topper's Solved these Questions
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
16 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - LONG ANSWER QUESTIONS
5 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
Similar Questions
Fluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The total pressure at the bottom of the container is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area s(s<<A) is punched on the veritical side of the containier at a height h(h<H/2)
The height hm at which the hole should be punched so that the liquid travels the maximum distance is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the Body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The density of the solid is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform cross sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation II:
A cyliner is removed and the original arrangement is restored.A tiny hole of area s(s<<A) is punched on the veritical sideof the containier at a height h(h<H/2)
The initial speed of efflux of the liquid at the hole is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.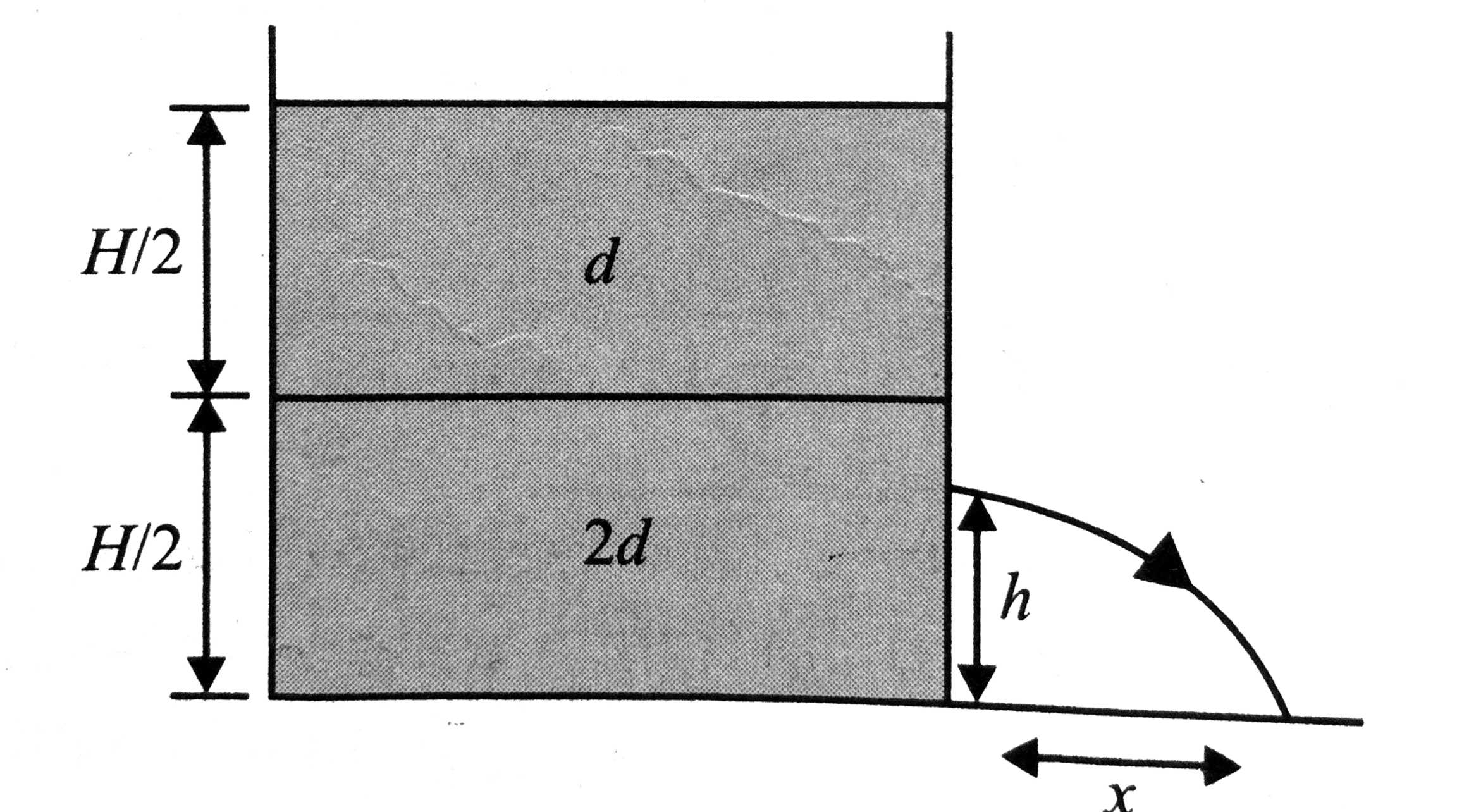
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area s(s<<A) is punched on the veritical sideof the containier at a height h(h<H/2)
The horizontal distance x travelled by the liquid is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the ody immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area s(s<<A) is punched on the veritical side of the container at a height h(h<H/2)
The maximum distance travelled xm is
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :
View SolutionA U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area=1cm2, It is filled with water of volume 60 cc. What volume of a liquid of density 4g/ should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube? a) 60 cc b) 45 cc c) 50 cc d) 35 cc
View SolutionAn open -ended U-tube of uniform cross-sectional area contains water (density 1.0g/cm23) standing initially 20 cm from the bottom in each arm. An immiscible liquid of density 4.0g/cm2 is added to one arm until a layer 5 cm high forms, as shown in the figure above. What is the ratio h2/h1 of the heights of the liquid in the two arms ?
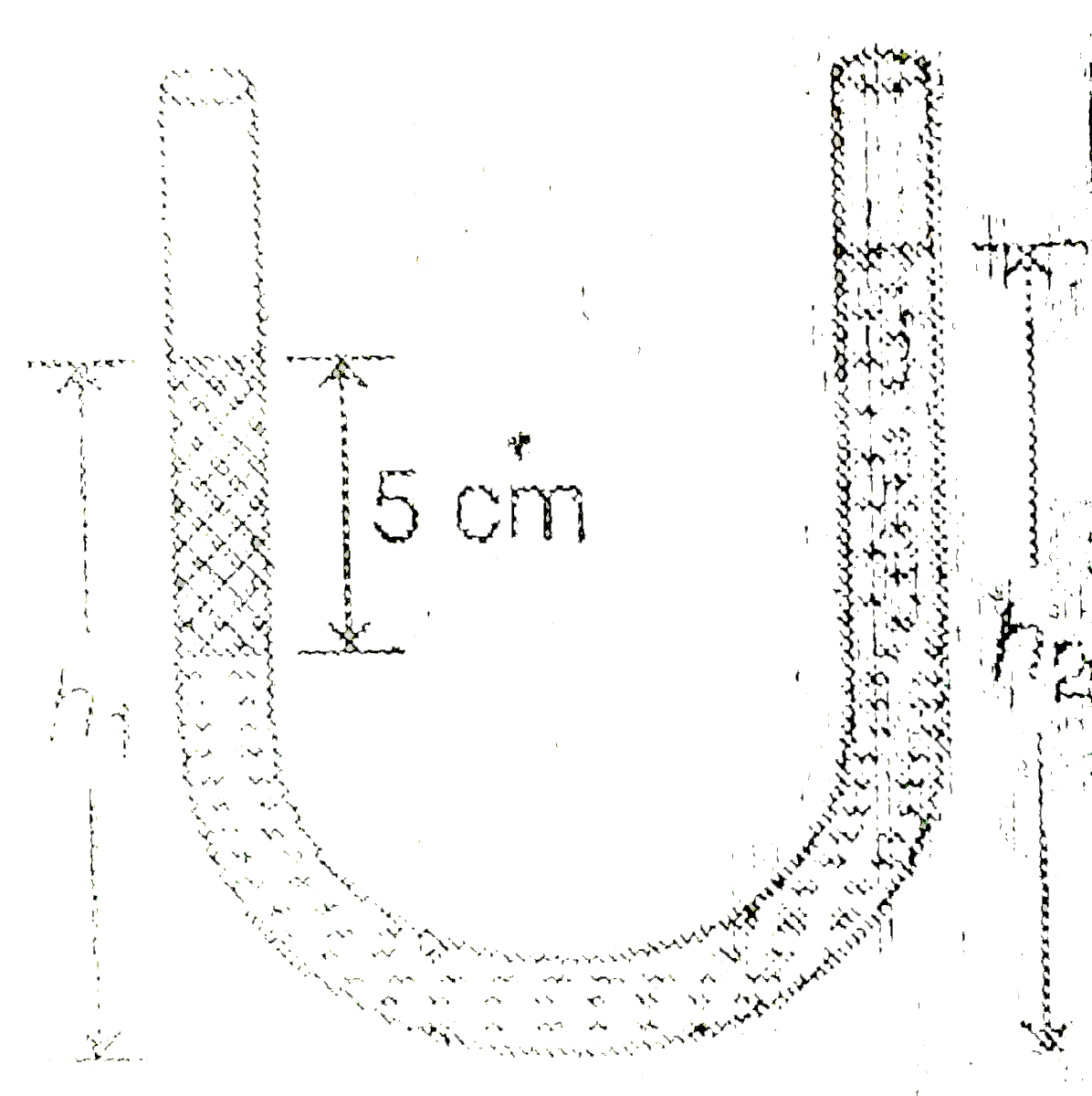
View Solution
