Consider four masses m1,m2,m3andm4arranged on the circumference of a circle as shown in figure below: Calculate:
(a) The gravitational potential energy of the system of 4 masses shown in figure.
(b) The gravitational potential at the point O due to all the 4 masses.

Text Solution
(a) The gravitational potential energy U (r ) of entire mass of the system
U=−Gm1m2r12−Gm1m3r13−Gm1m4r14−Gm2m3r23−Gm2m4r24−Gm3m4r34
Here r12,r13.... are distance between pair of particles
r214=R2+R2=2R2
r14=√2R=r12=r23=r24
r13=r24=2R
Substituting these distance values in above equation and we get :
U=−GR[m1m2√2+m1m22+m1m4√2+m2m3√2+m2m42+m3m4√2]
If all the masses are equal , then m1=m2=m3=m4=M
U=−GM2R[1√2+12+1√2+12+1√2]
U=−GM2R[1+4√2]
U=−GM2R[1+2√2]
(b) The gravitational potential are equal , then m1=m2=m3=m4=M
V0(r)=−Gm1R−Gm2R−Gm3R−Gm4R
If m1=m2=m3=m4=M
V0(r)=−4GMR

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - FULL MARKSCHAPTER - GRAVITATIONEXERCISE - TEXTUAL EVALUATION SOLVED (I. Multiple Choice Questions)15videos
GRAVITATION
- BOOK - FULL MARKSCHAPTER - GRAVITATIONEXERCISE - TEXTUAL EVALUATION SOLVED (II. Short Answer Questions)15videos
GRAVITATION
- BOOK - FULL MARKSCHAPTER - EXAMINATION QUESTION PAPER MARCH 2019EXERCISE - PART-IV10videos
EXAMINATION QUESTION PAPER MARCH 2019
- BOOK - FULL MARKSCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - ADDITIONAL QUESTIONS SOLVED (Numerical Problems)16videos
HEAT AND THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
From the figure, the gravitational potential at '0' due to three point masses is
AGml(2+1√2)BGml(√+12)C3GmlD2Gml - Question 2 - Select One
Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A−3Gm22bB−Gm22bC−3Gm2bD−Gm2b - Question 3 - Select One
A mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
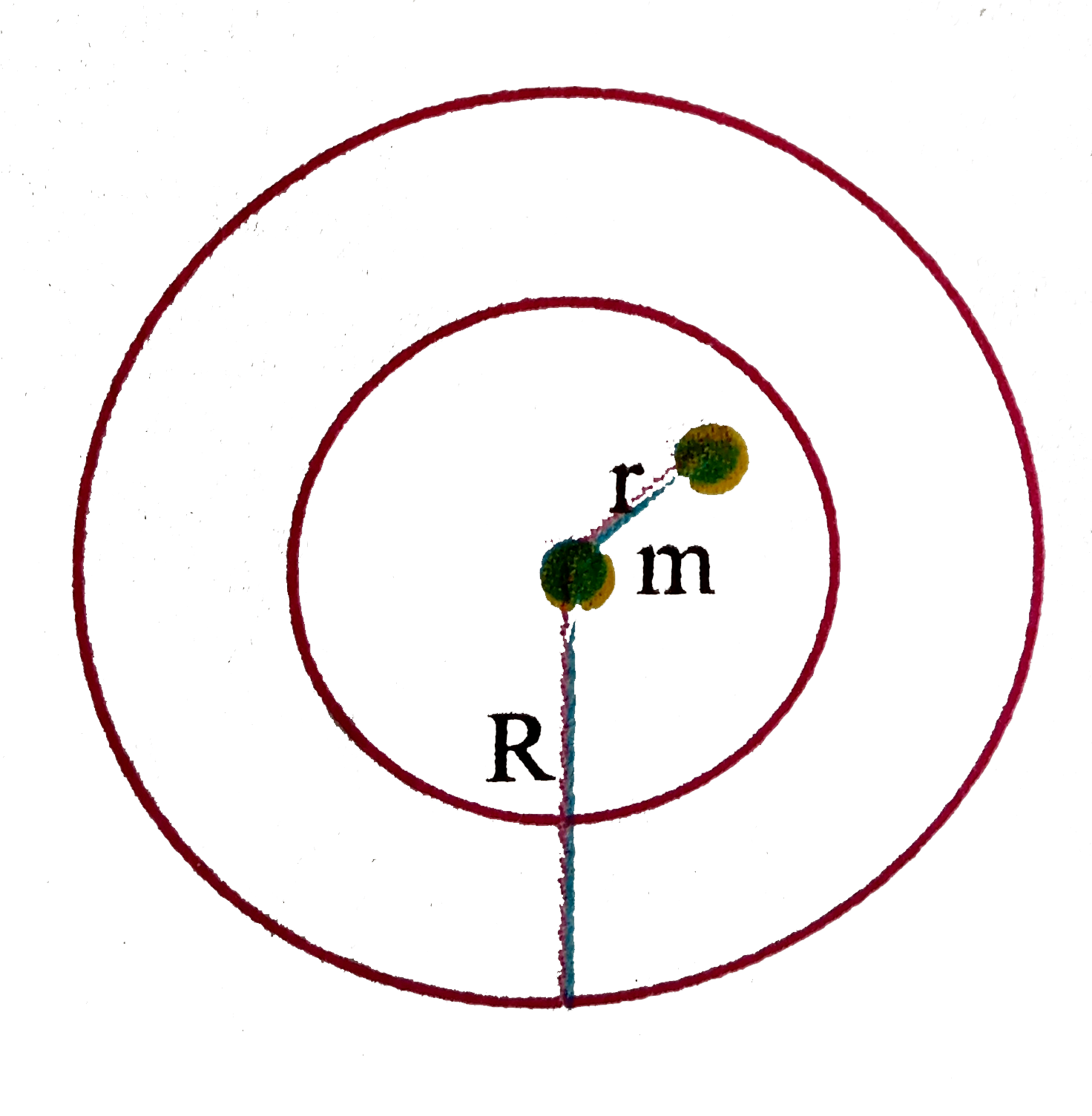 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero
Four particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionFind the gravitational potential energy of system consisting of uniform rod AB of mass M, length l and a point mass m as shown in figure.
 View Solution
View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
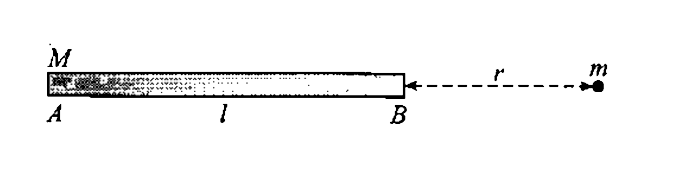 View Solution
View SolutionFigure shows 4 identical masses of mass m, arranged on a cube as shown.
The potential energy of the system is
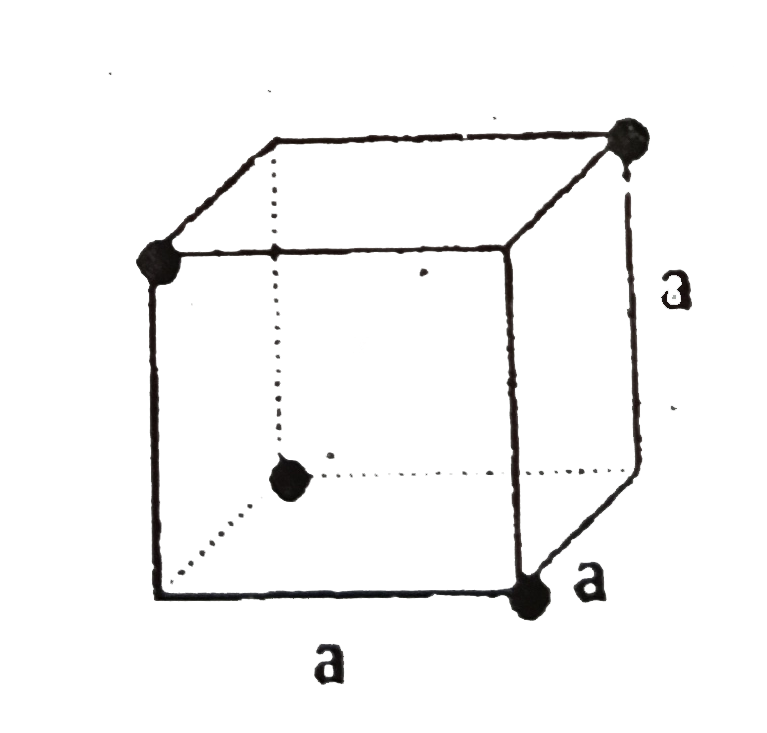 View Solution
View SolutionFigure shows 4 identical masses of mass m, arranged on a cube as shown.
The potential energy of the system is
 View Solution
View Solution

