Consider that an ideal gas (nmoles) is expanding in a process given by P=f(V), which passes through a point (P0,V0). Show that the gas is absorbing heat at (P0,V0) if the slope of the curve P=f(V) is larger than the slope of the adiabat passing through (p0,V0).
The slope of P=f(V)curve at(P0,V0)
The slope of an adiabat passing through (P0,V0)=−γP0V0
If dQ is the amount of heat absorbed in the process, P=f(V), then
dQ=dU+dW
or dQ=nCvdT+PdV….(i)
From PV=nRT,T=(1nR)PV=(1nR)f(V).V[∴P=f(V)]
∴dT(1nR)[f(V)dV+Vf'(V)dV]....(ii)
Using (ii) in (i), we get
dQdV=nCvdV[(1nR){f(V)dV+Vf'(V)dV}]+PdVdV
=CvR[f(V)+Vf'(V)]+P
At (P0,V0),dQdV=1γ−1[f(V0)+V0f'(V0)]+P0(AsRCv=γ−1)
As f(V0)=P0, therefore, at (P0,V0)
dQdV=V0f'(V0)γ−1+(1γ−1+1)P0=V0f'(V0)γ−1+γP0γ−1
=(1γ−1)[V0f'(V0)+γP0]
The gas will absorb heat at (P0,V0), when at (P0,V0)
dQdV>0i.e.,1γ−1[V0f'(V0)+γP0]>0
or V0f'(V0)+γP0>0orf'(V0)>−γP0V0
which is the required result.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Higher order thinking skills
9 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Value based Questions
4 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Short answer questions(NCERT)
6 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assertion-Reason Type Questions
24 Videos
Similar Questions
Consider that an idela gas (n mole) is espanding in a process gives by p=f(v), which passes throught a point (V0,p0). Shown that the gas is absorbing heat at (p0,v0) if the slope of the curve p=f(v) is large than the slope of the adabatic passing throught (p0,v0).
View SolutionA curve y=f(x) passes through point P(1,1) . The normal to the curve at P is a (y−1)+(x−1)=0 . If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, then the equation of the curve is
View Solution
Knowledge Check
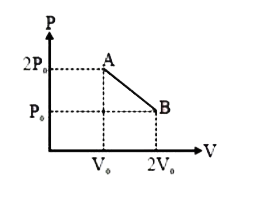
2 moles of ideal monatomic gas is carried from a state (P0,V0) to a state (2P0,2V0) along a straight line path in a P- V diagram. The amount of heat absorbed by
A3P0V0B92P0V0C6P0V0D32P0V0An ideal gas is transformed from state A(P1,V1) to the state B(P2,V2) through path AB. In this process the work done by the gas is
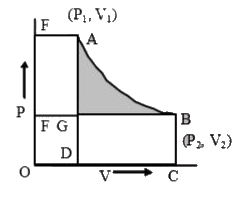 AW = area ABCDABW = area ABEFACW = area ABGADW = area ABCOFA
AW = area ABCDABW = area ABEFACW = area ABGADW = area ABCOFAOne mole of a mono- atomic ideal gas undergoes a quasi- static process, which is depicted by a straight line joining points (V0T0) and (2V0,3T0) in a V - T diagram . What is the value of the heat capacity of the gas at the point (V0,T0) ?
ARB32RC2RD0
n' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will is p0v04nR then value of N is:
View SolutionShow that the entropy of a perfect gas can be written as S=CvInp+CpInV+S0 where S0 is a constant.
View SolutionFor an ideal gas the slope of V-T graph during an adiabatic process is (dV)/(dT) = -matap∮wherevolumeandtemperatureareV_(0)andT_(0).F∈dthevalueofC_(p) of the gas. It is given that m is a positive number.
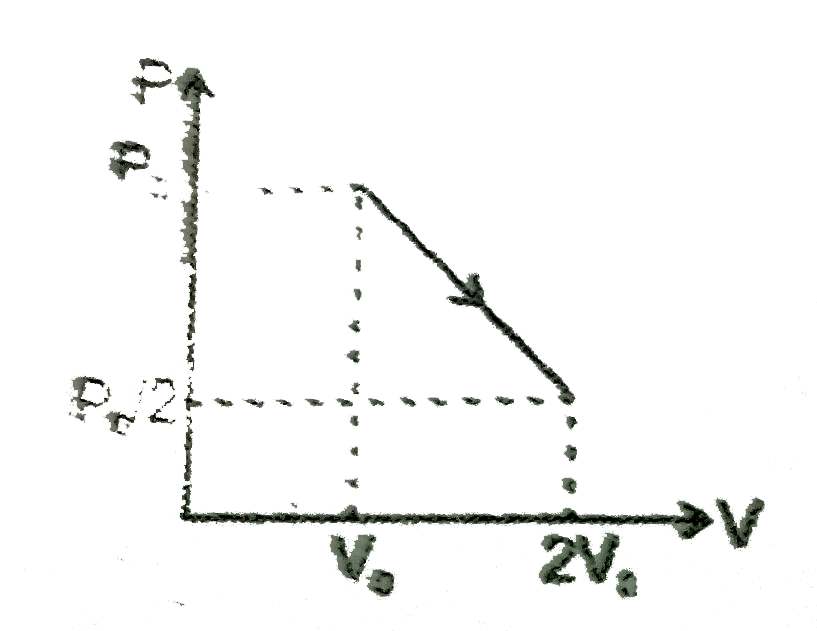
View SolutionAn ideal monatomic gas is at P0,V0. It is taken to final volume 2V0 when pressure is P0/2 in a process which is straight line on P−V diagram. Then
View SolutionThe internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
The heat absorbed by the gas in the process is
View Solution
