Consider the charges q, q and -q placed at vertices of an equilateral triangle as shown it figure. What is the force on each charge ? Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

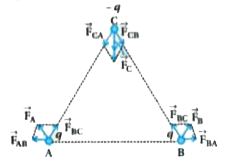
Situation given in the statement is depicted in the following figure.
Here $| q_{1} | = | q_{2} | = | q_{3} | = q$

Here since AABC is an equilateral triangle, we have AB = BC = CA = I
Magnitudes of mutual Coulombian forces are equal to F.
$F_{12} = F_{21} = F_{23} = F_{13} = F_{31} = F = \frac{k q^{2}}{l^{2}}$ ....(1)
Resultant Coulombian force on $q_{1}$ is:
${\to F}_{1} = {\to F}_{12} + {\to F}_{13}$
$∴ F_{1} = \sqrt{F^{2} + F^{2} + 2 F F cos (120^{\circ})} (∴ F_{12} = F_{13} = F)$
$= \sqrt{2 F^{2} + 2 F^{2} (- \frac{1}{2})}$ (Here, $θ = 120^{\circ}$ )
$= \sqrt{F^{2}}$
$∴ F_{1} = F$ (in the direction parallel to $¯ ¯¯¯¯ ¯ B C$ ).....(2)
Resultant Coulombian force on $q_{3}$ is,
${\to F}_{3} = {\to F}_{31} + {\to F}_{32}$
$∴ F_{3} = \sqrt{F^{2} + F^{2} + 2 F F {cos 60}^{\circ}} (∴ F_{31} = F_{32} = F)$
$∴ F_{3} = \sqrt{2 F^{2} + 2 F^{2} (\frac{1}{2})}$ (Here $θ = 60^{\circ}$ )
$= \sqrt{3 F^{2}}$
$∴ F_{3} = \sqrt{3 F}$ (in the direction of $- - \to C D$ )
where D is the midpoint of $¯ ¯¯¯¯ ¯ A B$ ) (or along the direction bisecting $∠ (A C B)$ )
$∴ {\to F}_{B} = {(F {cos 60}^{\circ}) (- ˆ i) + (F {sin 60}^{\circ} ˆ j)} + F {cos 60}^{\circ} ˆ i + F {sin 60}^{\circ} ˆ j + \sqrt{3} F (- ˆ j)$
$= - \frac{F}{2} ˆ i + \frac{\sqrt{3}}{2} F ˆ j + \frac{F}{2} ˆ i + \frac{\sqrt{3}}{2} F ˆ j - \sqrt{3} F ˆ j$
$= \sqrt{3} F ˆ j - \sqrt{3} F ˆ j$
$∴ {\to F}_{B} = \to 0$
$∴ {\to F}_{B} = 0$
Here, if given point charges have equal mass then resultant gravitational force on this isolated system will also be zero.
Another alternative Method (Aliter) :
Here, resultant Coulombian force acting on whole system is,
${\to F}_{B} = {\to F}_{1} + {\to F}_{2} + {\to F}_{3}$
$∴ = ({\to F}_{12} + {\to F}_{13} + {\to F}_{21} + {\to F}_{23} + {\to F}_{31} + {\to F}_{32})$
$= ({\to F}_{12} + {\to F}_{21}) + ({\to F}_{13} + {\to F}_{31}) + ({\to F}_{23} + {\to F}_{32})$
$= \to 0 + \to 0 + \to 0$
$= \to 0$ ( $∴$ According to Newton.s third law)
${\to F}_{12} = - {\to F}_{21} . {\to F}_{13} = - {\to F}_{31}$ and ${\to F}_{23} = - {\to F}_{32}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTRIC CHARGES AND FIELDS -SECTION B NUMERICALS (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)

Home
Ask Doubt
Profile