Consider the decay of a free neutron at rest: n⊤+e− Show that the tow-body dacay of this type must necessarily give an electron of fixed energy and, therefore, cannot for the observed continous energy distribution in the β-decay of a neutron or a nucleus.
In the decay process, n→p+e
energy of electron is equal to (Δm)c2
whereΔm= mass defect = mass of neutron − mass of proton and electron ,
which is fixed. Therefore, two body decay of this type cannot explain the observed continuous energy distribution in the β− decay of a neutron in a nucleus.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Additional Exercises
3 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - higher order thinking skills
10 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Advanced Problems For Competitions
20 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Consider the decay of a free neutron at rest: n⊤+e− Show that the tow-body dacay of this type must necessarily give an electron of fixed energy and, therefore, cannot for the observed continous energy distribution in the β-decay of a neutron or a nucleus.

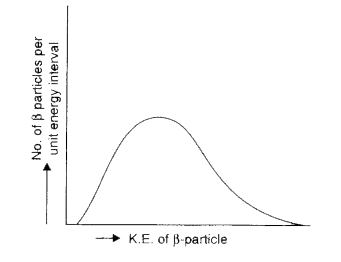
View SolutionDraw the graph showing distribution of kinetic energy of electrons emitted during beta decay.
View Solution
Knowledge Check
During alpha-decay , a nucleus decays by emitting an α-particle ( a helium nucleus .2He4) according to the equation
.AZX→.A−4Z−2Y+.42He+Q
In this process, the energy released Q is shared by the emitted α-particle and daughter nucleus in the form of kinetic energy .
The energy Q is divided in a definite ratio among the α-particle and the daughter nucleus .
A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo β-decay .This process also involves a release of definite energy . Initially, the β-decay was represented as .AZX→.AZ+1Y+e−(electron)+Q
According to this reaction, the energy released during each decay must be divided in definite ratio by the emitted e' (β-particle) and the daughter nucleus. While , in alpha decay, it has been found that every emitted α-particle has the same sharply defined kinetic energy. It is not so in case of β-decay . The energy of emitted electrons or positrons is found to vary between zero to a certain maximum value. Wolfgang Pauli first suggested the existence of neutrinoes in 1930. He suggested that during β-decay, a third particle is also emitted. It shares energy with the emitted β particles and thus accounts for the energy distribution.
During β+ decay (positron emission) a proton in the nucleus is converted into a neutron, positron and neutrino. The reaction is correctly represented asA.AZX→.A−1Z−1X+e++v+ EnergyB.AZX→. AZ−1X+e++v+ EnergyC.AZX→.AZ−1X+e++v+ EnergyD.AZX→.A−1ZX+e++v+ EnergyThe β-decay process, discovered around 1900, is basically the decay of a neutron (n), In the laboratory, a proton (p) and an electron (e−) are observed as the decay products of the neutron. Therefore, considering the decay of a neutron as a tro-body dcay process, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process i.e., n→p+e−+−ve, around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (−Ve) to be massless and possessing negligible energy, and neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8×106eV. The kinetic energy carried by the proton is only the recoil energy.
What is the maximum energy of the anti-neutrino?AzeroBMuch less than 0.8×106eVCNearly 0.8×106eVDMuch larger than 0.8×106eVThe β-decay process, discovered around 1900, is basically the decay of a neutron (n), In the laboratory, a proton (p) and an electron (e−) are observed as the decay products of the neutron. Therefore, considering the decay of a neutron as a tro-body dcay process, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process i.e., n→p+e−+−ve, around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (−Ve) to be massless and possessing negligible energy, and neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8×106eV. The kinetic energy carried by the proton is only the recoil energy.
If the anti-neutrino has a mass of 3eV/c2 (where c is the speed of light) instead of zero mass, what should be the range of the kinetic energy, K of the electron?A0≤K≤0.8×106eVB3.0eV≤K≤0.8×106eVC3.0eV≤K<0.8×106eVD0≤K<0.8×106eV
Draw the graph showing distribution of kinetic energy of electrons emitted during beta decay.
View SolutionSTATEMENT-1 : In the decay of a free neutron at rest, into a proton and electron, it has been predicated that a third particle must also be emitted because the emitted electrons do not have a definite kinetic energy.
and
STATEMENT-2 : For the simple decay of a stationary particle into two moving particles, the kinetic energies of the particle must have a sharply defined value.
View SolutionA neutron at rest decays. Assuming the resulting proton to remain at rest, too, find the kinetic energy of the electron and the energy of the antineutrino.
View SolutionBefore the neutrino hypothesis the beta decay process was throught to be the transition.
n→p+¯e
If this was true show that if the neutron was at rest the proton and electron would emerge with fixed energies and calculate them. Experimentally the electron energy was found to have a large range.
View SolutionOne of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy.
The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state.
Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively.
When electrons return form n2 to n1 state, the number of lines in the spectrum will equal to
(n2−n1)(n2−n1+1)2
If the electon comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as :
E2−E1=ΔE,δE⇒hcλ
Since, h and c are constant, δE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula
¯v=R(1n21−1n22).
where R is a Rydberg's constant (R=1.1×107m−1)
An electron in H-atom in M-shell on de-excitation to ground state gives maximum ........... spectrum lines.
View Solution
