Consider the following conclusiond regarding the components of an electric field at a certain point in space given by Ex=−Ky,Ey=Kx,Ez=0 .
The field is conservative.
The field is nonconservative.
The lines of force are straight lines.
The lines of force are circles.
The correct Answer is:B, D
To solve the problem regarding the electric field components given by Ex=−Ky,Ey=Kx,Ez=0, we need to determine whether this electric field is conservative. A field is conservative if the curl of the field is zero. Let's go through the steps to find the curl of the electric field.
Step 1: Write down the electric field components
The electric field components are given as:
- Ex=−Ky
- Ey=Kx
- Ez=0
Step 2: Set up the curl of the electric field
The curl of a vector field E is given by the formula:
∇×E=∣∣
∣
∣∣^i^j^k∂∂x∂∂y∂∂zExEyEz∣∣
∣
∣∣
Substituting the components of the electric field:
∇×E=∣∣
∣
∣∣^i^j^k∂∂x∂∂y∂∂z−KyKx0∣∣
∣
∣∣
Step 3: Calculate the determinant
Calculating the determinant, we expand it as follows:
∇×E=^i(∂∂y(0)−∂∂z(Kx))−^j(∂∂x(0)−∂∂z(−Ky))+^k(∂∂x(Kx)−∂∂y(−Ky))
Step 4: Evaluate each term
1. For the ^i component:
∂∂y(0)−∂∂z(Kx)=0−0=0
2. For the ^j component:
∂∂x(0)−∂∂z(−Ky)=0−0=0
3. For the ^k component:
∂∂x(Kx)−∂∂y(−Ky)=K−(−K)=K+K=2K
Step 5: Combine the results
Thus, we find:
∇×E=0^i−0^j+2K^k=2K^k
Step 6: Conclusion
Since the curl of the electric field ∇×E is not zero (it is 2K^k), the electric field is not conservative.
Final Answer
The electric field is not conservative.
---
The electric field components are given as:
- Ex=−Ky
- Ey=Kx
- Ez=0
The curl of a vector field E is given by the formula:
∇×E=∣∣
∣
∣∣^i^j^k∂∂x∂∂y∂∂zExEyEz∣∣
∣
∣∣
Substituting the components of the electric field:
∇×E=∣∣
∣
∣∣^i^j^k∂∂x∂∂y∂∂z−KyKx0∣∣
∣
∣∣
Calculating the determinant, we expand it as follows:
∇×E=^i(∂∂y(0)−∂∂z(Kx))−^j(∂∂x(0)−∂∂z(−Ky))+^k(∂∂x(Kx)−∂∂y(−Ky))
1. For the ^i component:
∂∂y(0)−∂∂z(Kx)=0−0=0
2. For the ^j component:
∂∂x(0)−∂∂z(−Ky)=0−0=0
∂∂x(Kx)−∂∂y(−Ky)=K−(−K)=K+K=2K
Thus, we find:
∇×E=0^i−0^j+2K^k=2K^k
Since the curl of the electric field ∇×E is not zero (it is 2K^k), the electric field is not conservative.
The electric field is not conservative.
Similar Questions
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
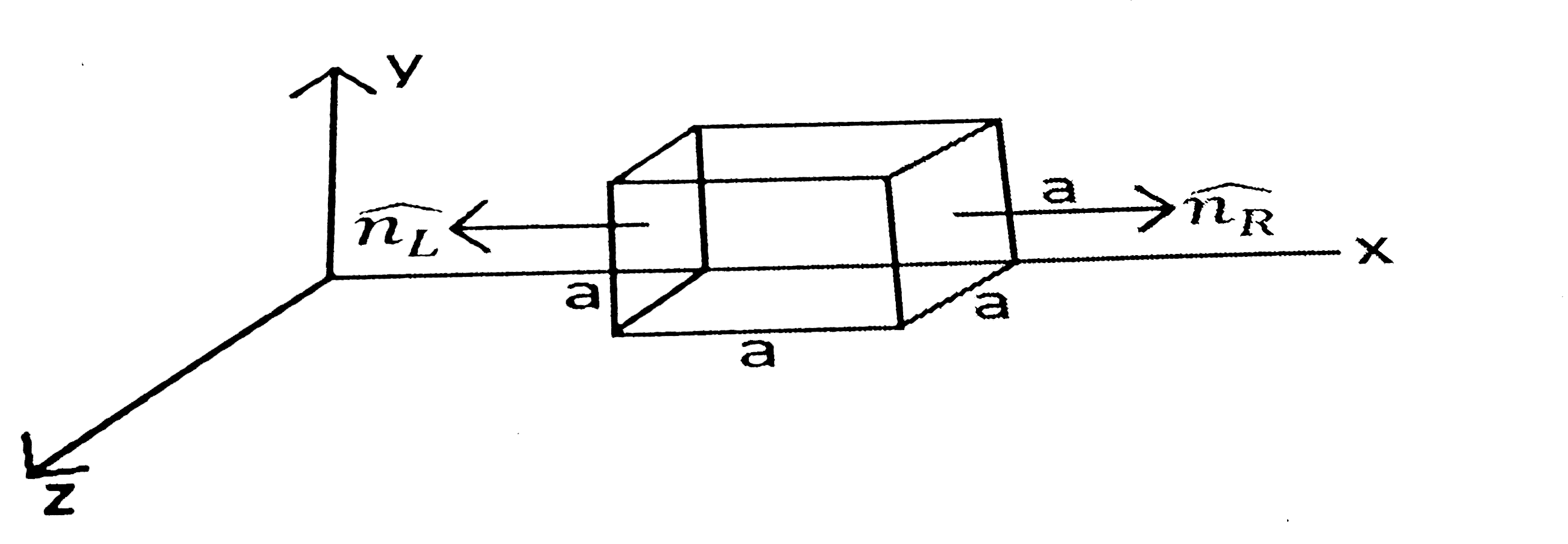
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
 View Solution
View SolutionA cube is arranged such that its length, breadth and height are along X, Y and Z directions, One of its corners is situated a the origin. Length of each side of the cube is 25cm. The components of electric field are Ex=400√2N/C,Ey=0andEz=0 respectively. Find the flux coming out of the cube at one end.
View SolutionAn electric dipole coincides on Z-axis and its mid-point is on origin of the coordinates system. The electric field at an axial point at a distance z from origin is E(z) and electric field at an equatorial point at a distance y from origin is E(y). Here, z=y>>a, so ∣∣∣E(z)E(y)∣∣∣=... 1 4 3 2
View SolutionThe electric field and the electric potential at a point are E and V respectively.
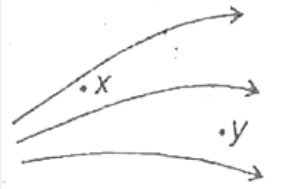
View SolutionFigure shows electric lines of force. If Ex and Ey are the magnitudes of electric field at points x and y respectively, then
 View Solution
View SolutionIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A: If E be electric field at a point , in free space then energy density at that point will be 12ε0E2 .
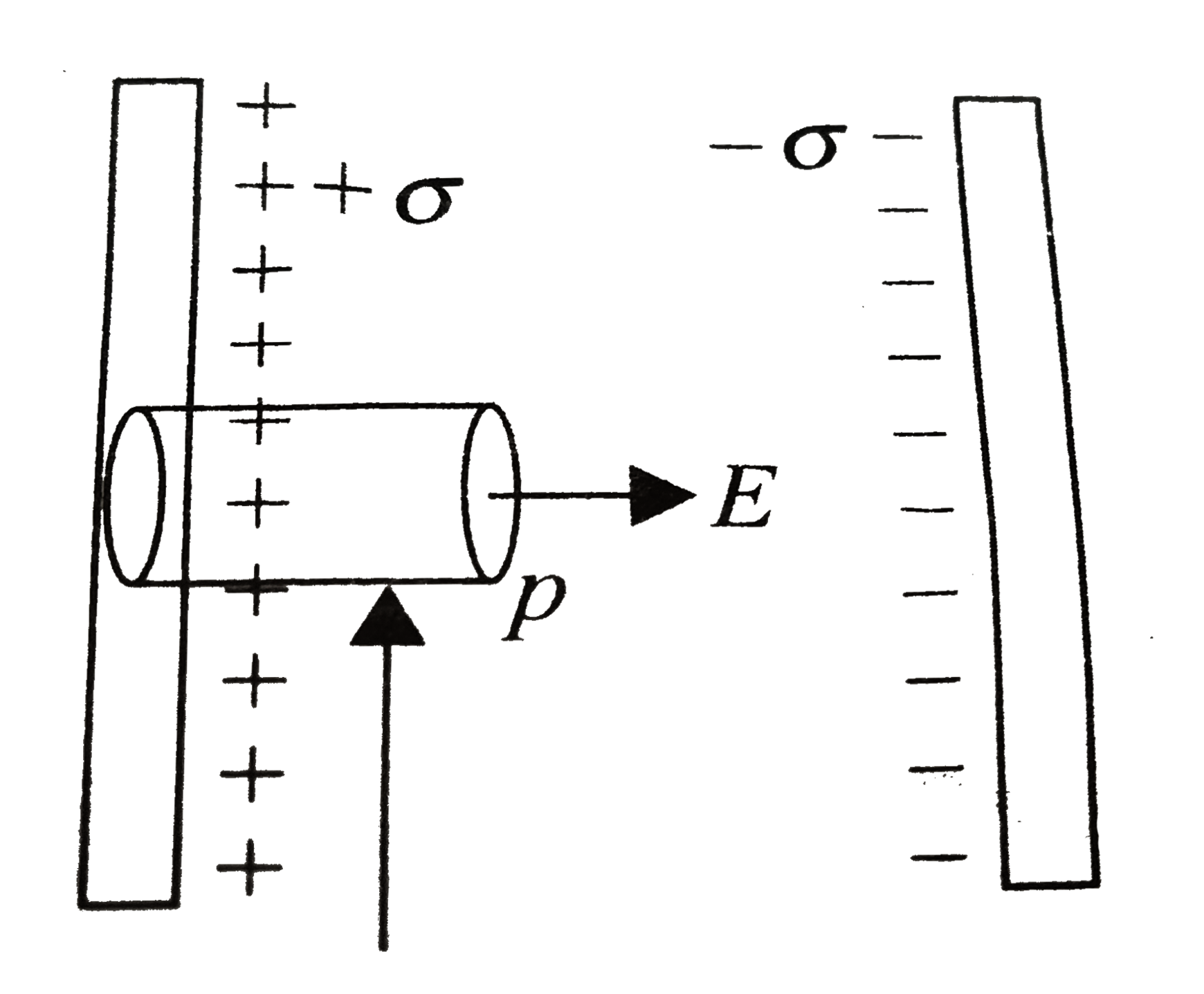
R , electrostatic field is a conservative field .View SolutionConsider the situation shown in figure. We find electric field E at point P using Gauss's law and it comes out to be E=σ/ε0. This electric field is due to
 View Solution
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
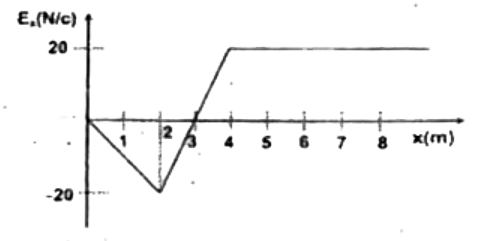 View Solution
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
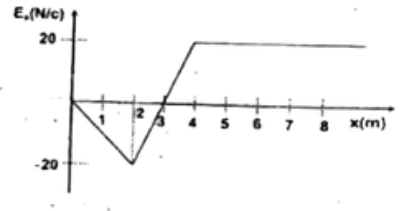
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m isView SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
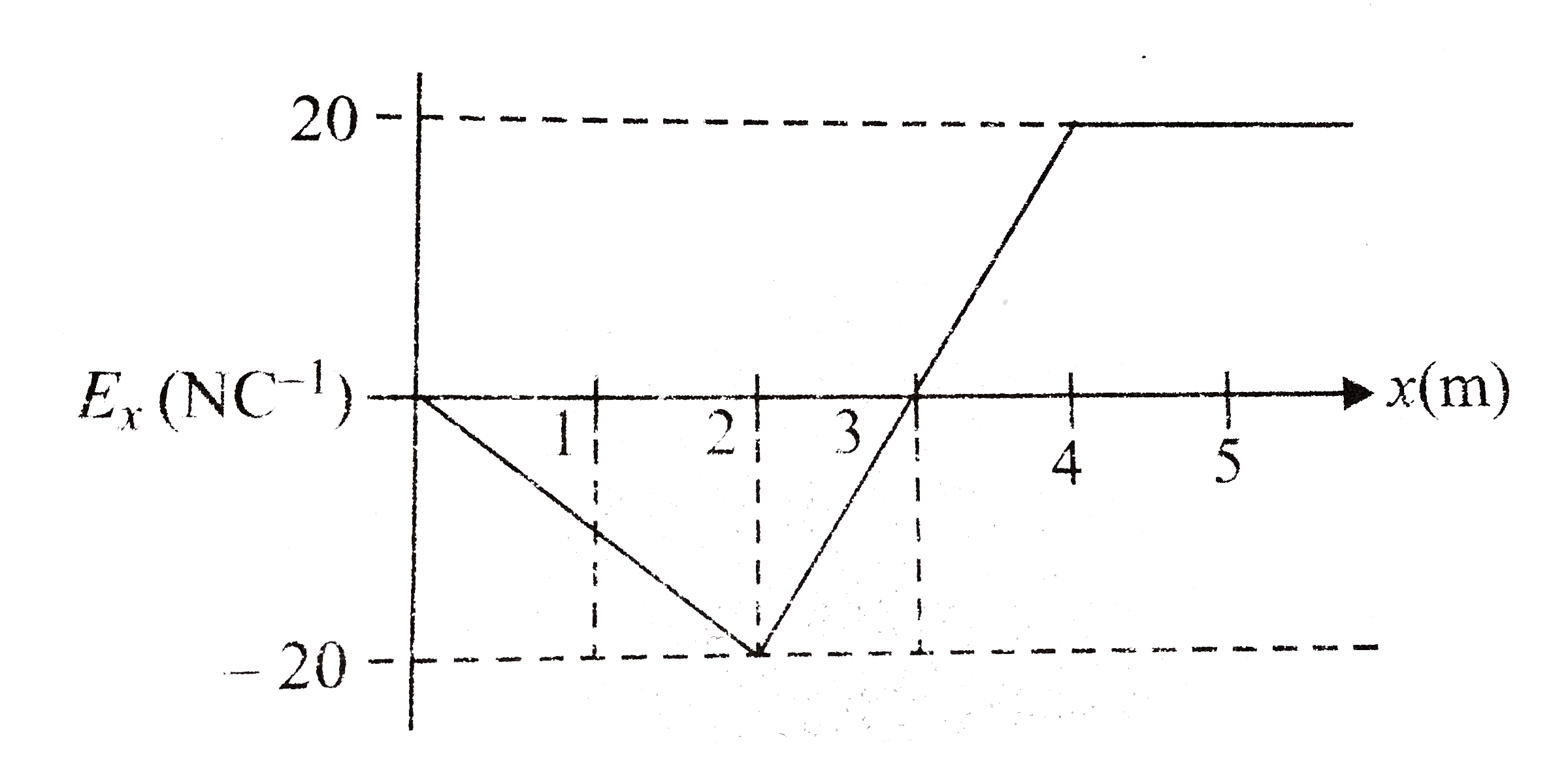 View Solution
View Solution
