Consider the following nuclear decay:
If the uranium is at rest before its decay, which one of the following statements is true concerning the final nuclei?
They have equal kinetic energies, but he thorium nucleus has much more momentum.
They have momenta of equal magnitudes, but the thorium nucleus has much more kinetic energy.
They have equal kinetic energies and momenta of equal magnitudes
They have momenta of equal magnitudes, but X has much more kinetic energy
The correct Answer is:D
To solve the problem regarding the nuclear decay of Uranium-236 into Thorium-234 and another particle (X), we need to analyze the conservation laws that apply during this decay process.
1. Identify the Decay Process:
The decay can be represented as:
Uranium-236→Thorium-234+X
Here, X represents the other particle produced during the decay.
2. Conservation of Mass Number:
The mass number (A) must be conserved in nuclear reactions. The mass number of Uranium-236 is 236, and Thorium-234 has a mass number of 234. Thus, we can find the mass number of particle X:
AU=ATh+AX⟹236=234+AX⟹AX=2
Therefore, X is a particle with a mass number of 2, which indicates that X is likely an alpha particle (42He).
3. Conservation of Atomic Number:
The atomic number (Z) must also be conserved. The atomic number of Uranium-236 is 92, and Thorium-234 has an atomic number of 90. Thus, we can find the atomic number of particle X:
ZU=ZTh+ZX⟹92=90+ZX⟹ZX=2
This confirms that X is indeed an alpha particle, as it has an atomic number of 2.
4. Kinetic Energy and Momentum Considerations:
Since the uranium nucleus is initially at rest, the total momentum before decay is zero. According to the conservation of momentum:
Momentum of Thorium+Momentum of X=0
This implies that the momentum of Thorium and the momentum of X are equal in magnitude but opposite in direction:
pTh=−pX
5. Kinetic Energy Comparison:
The kinetic energy of a particle is given by the formula:
KE=p22m
Since pTh=−pX, we can express the kinetic energies in terms of their masses:
KETh=p2Th2mTh,KEX=p2X2mX
Given that mX (mass of alpha particle) is less than mTh (mass of Thorium), the kinetic energy of X will be greater than that of Thorium.
6. Conclusion:
Therefore, the correct statement concerning the final nuclei is that they have momenta of equal magnitudes, but the kinetic energy of X is greater than that of Thorium.
Final Answer:
The correct statement is: "They have momenta of equal magnitudes, but the kinetic energy of X is more as compared to Thorium."
The decay can be represented as:
Uranium-236→Thorium-234+X
Here, X represents the other particle produced during the decay.
The mass number (A) must be conserved in nuclear reactions. The mass number of Uranium-236 is 236, and Thorium-234 has a mass number of 234. Thus, we can find the mass number of particle X:
AU=ATh+AX⟹236=234+AX⟹AX=2
Therefore, X is a particle with a mass number of 2, which indicates that X is likely an alpha particle (42He).
The atomic number (Z) must also be conserved. The atomic number of Uranium-236 is 92, and Thorium-234 has an atomic number of 90. Thus, we can find the atomic number of particle X:
ZU=ZTh+ZX⟹92=90+ZX⟹ZX=2
This confirms that X is indeed an alpha particle, as it has an atomic number of 2.
Since the uranium nucleus is initially at rest, the total momentum before decay is zero. According to the conservation of momentum:
Momentum of Thorium+Momentum of X=0
This implies that the momentum of Thorium and the momentum of X are equal in magnitude but opposite in direction:
pTh=−pX
The kinetic energy of a particle is given by the formula:
KE=p22m
Since pTh=−pX, we can express the kinetic energies in terms of their masses:
KETh=p2Th2mTh,KEX=p2X2mX
Given that mX (mass of alpha particle) is less than mTh (mass of Thorium), the kinetic energy of X will be greater than that of Thorium.
Therefore, the correct statement concerning the final nuclei is that they have momenta of equal magnitudes, but the kinetic energy of X is greater than that of Thorium.
The correct statement is: "They have momenta of equal magnitudes, but the kinetic energy of X is more as compared to Thorium."
Topper's Solved these Questions
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS(Matrix - Match)
14 Videos
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS(Integer Type)
7 Videos
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
22 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS
72 Videos
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
11 Videos
Similar Questions
Consider the following nuclear decay: (initially .236U92 is at rest)
.23692→23290Th→X
If the uranium is at rest before its decay, which one of the following statement is true concerning the final nuclei ?
View Solution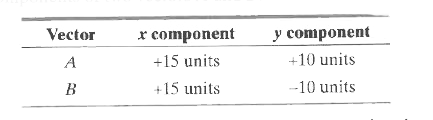
Which one of the following statements concerning these vectors is true ?
View Solution
Knowledge Check
Consider the following nuclear decay: 23692U→23290Th+X
What is X?Aα decayBpCβ+Dβ−Which one of the following statements is true concerning scalar quantities ?
AScalar quantities must be represented by base units.BScalar quantities have both magnitude and direction.CScalar quantities can be added to vector quantities using rules of trigonometry.DScalar quantities can be added to other scalar quantities using rules of ordinary addition.Which one of the following statements is true for nuclear forces?
AThey are short range forcesBThey are equal in strength to electrostatic forcesCThey obey the inverse third power law of distanceDThey obey the inverse square law of distance
Which one of the following statements concerning momentum is true?
View SolutionWhich one of the following statements concerning a convex mirror is true?
View SolutionWhich one of the following statements is true about an organism and its classification ?
View SolutionWhich one of the following statement is true concerning an object executing simple harmonic motion?
View SolutionWhich one of the following statement is true about an organism and its classficiation.
View Solution
