Consider the points lying on a straight line joining two fixed opposite charges. Between the charges there is
No point where electric field is zero
Only one point where electric field is zero
No point where potential is zero
Only one point where potential is zero
To solve the problem regarding the electric field and electric potential between two fixed opposite charges, let's break it down step by step.
1. Understanding the Setup:
- We have two fixed charges: one positive charge Q1 and one negative charge Q2 (where Q2=−Q).
- They are separated by a distance d.
2. Electric Field Between the Charges:
- The electric field E due to a point charge is given by the formula:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge.
- In the region between the two charges, the electric field due to Q1 (positive) points away from Q1 and the electric field due to Q2 (negative) points towards Q2.
3. Direction of Electric Fields:
- Since both electric fields are in the same direction (from the positive charge to the negative charge), they will add up.
- Therefore, the resultant electric field Enet at any point between the charges is not zero:
Enet=EQ1+EQ2>0
- This means there is no point between the charges where the electric field is zero.
4. Electric Potential Between the Charges:
- The electric potential V at a point due to a charge is given by:
V=kQr
- The total potential Vnet at any point between the charges can be expressed as:
Vnet=VQ1+VQ2=kQ1r1+kQ2r2
- Here, r1 is the distance from Q1 to the point and r2 is the distance from Q2 to the point.
5. Finding the Point Where Potential is Zero:
- Set the total potential to zero:
Vnet=kQ1r1+kQ2r2=0
- This leads to:
Q1r1+Q2r2=0
- Rearranging gives:
Q1r1=−Q2r2
- This indicates that there is only one point between the charges where the potential is zero, which occurs when the magnitudes of the potentials due to each charge are equal.
6. Conclusion:
- Therefore, we conclude that:
- There is no point where the electric field is zero between the charges.
- There is only one point where the electric potential is zero.
Final Answer:
- No point where electric field is zero and only one point where potential is zero.
- We have two fixed charges: one positive charge Q1 and one negative charge Q2 (where Q2=−Q).
- They are separated by a distance d.
- The electric field E due to a point charge is given by the formula:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge.
- In the region between the two charges, the electric field due to Q1 (positive) points away from Q1 and the electric field due to Q2 (negative) points towards Q2.
- Since both electric fields are in the same direction (from the positive charge to the negative charge), they will add up.
- Therefore, the resultant electric field Enet at any point between the charges is not zero:
Enet=EQ1+EQ2>0
- This means there is no point between the charges where the electric field is zero.
- The electric potential V at a point due to a charge is given by:
V=kQr
- The total potential Vnet at any point between the charges can be expressed as:
Vnet=VQ1+VQ2=kQ1r1+kQ2r2
- Here, r1 is the distance from Q1 to the point and r2 is the distance from Q2 to the point.
- Set the total potential to zero:
Vnet=kQ1r1+kQ2r2=0
- This leads to:
Q1r1+Q2r2=0
- Rearranging gives:
Q1r1=−Q2r2
- This indicates that there is only one point between the charges where the potential is zero, which occurs when the magnitudes of the potentials due to each charge are equal.
- Therefore, we conclude that:
- There is no point where the electric field is zero between the charges.
- There is only one point where the electric potential is zero.
- No point where electric field is zero and only one point where potential is zero.
Topper's Solved these Questions
- ELECTROSTATICS BOOK - ERRORLESS CHAPTER - ELECTROSTATICS EXERCISE - Ordinary Thinking Objective Questions (Electric Dipole)
38 Videos
- ELECTROSTATICS BOOK - ERRORLESS CHAPTER - ELECTROSTATICS EXERCISE - Ordinary Thinking Objective Questions (Electric Flux and Gauss.s Law)
28 Videos
- ELECTROSTATICS BOOK - ERRORLESS CHAPTER - ELECTROSTATICS EXERCISE - Ordinary Thinking Objective Questions (Electric Flux and Gauss.s Law)
28 Videos
- ELECTRONICSBOOK - ERRORLESS CHAPTER - ELECTRONICSEXERCISE - Selv Evaluation Test
23 Videos
- HEATING AND CHEMICAL EFFECT OF CURRENTBOOK - ERRORLESS CHAPTER - HEATING AND CHEMICAL EFFECT OF CURRENTEXERCISE - Self Evaluation Test
14 Videos
Similar Questions
Assertion At the centre of the line joining two equal and opposite charges, E=0
Reason At the centre of the line joining two equal and similar charge, E≠0.
View SolutionTwo point charges +4μCand+1μC are separated by a distance of 2 m in air. Find the point on the line joining the two charges at which the net electric field of the system is zero.
View Solution
Knowledge Check
At any point on the right bisector of line joining two equal and opposite charges
Athe electric field is zeroBthe electric potential is zeroCthe electric potential decreases with increasing distance from centreDthe electric field is perpendicular to the line joining the chargesTwo point charges are kept at a certain distance from one another. The graph represents the variartion of the potential along the straight line connecting the two charges. At what point is the electric field zero ?
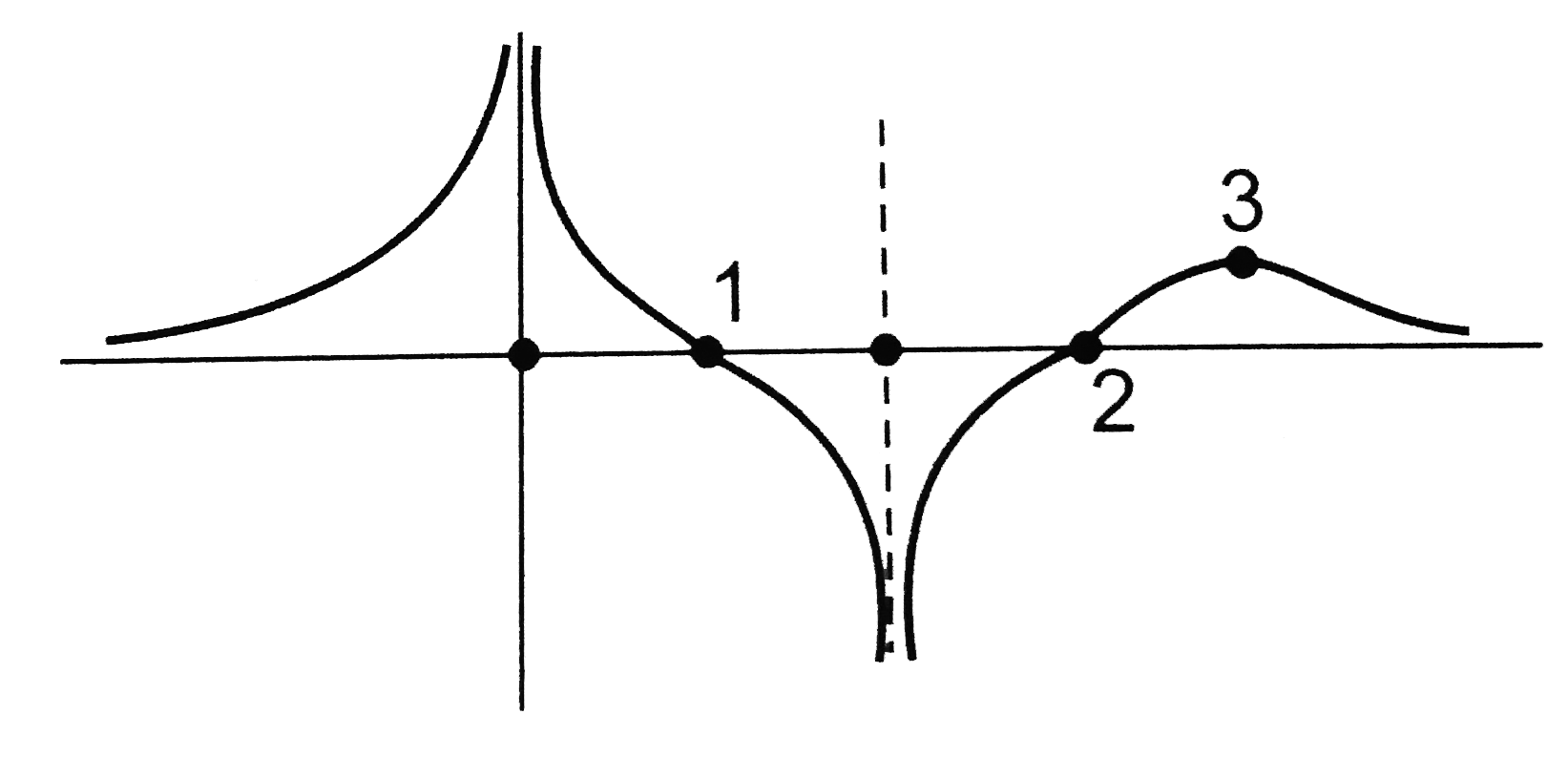 A1B2C3Dnone of these
A1B2C3Dnone of theseA charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium , if q is equal to
A−Q2B−Q4C+Q4D+Q2
Two equal charges, +Q each, are at a distance r from each other. A third charge is placed on the line joining the above two charges such that all these charges are in equilibrium. Find q, in terms of Q.
View SolutionTwo point objects carry positive charges of magnitude 5e and 20e . Separation between the charges is 1 cm. Find the location of points on the line joining the two charges where the electric field intensity is zero.
View SolutionDistinguish between fixed charge and floating charge.
View SolutionA charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
View SolutionTwo point charges q1=+2C and q2=−1C are separated by a distance d. The position on the line joining the two charges where a third charge q=+1C will be in equilibrium is at a distance
View Solution
