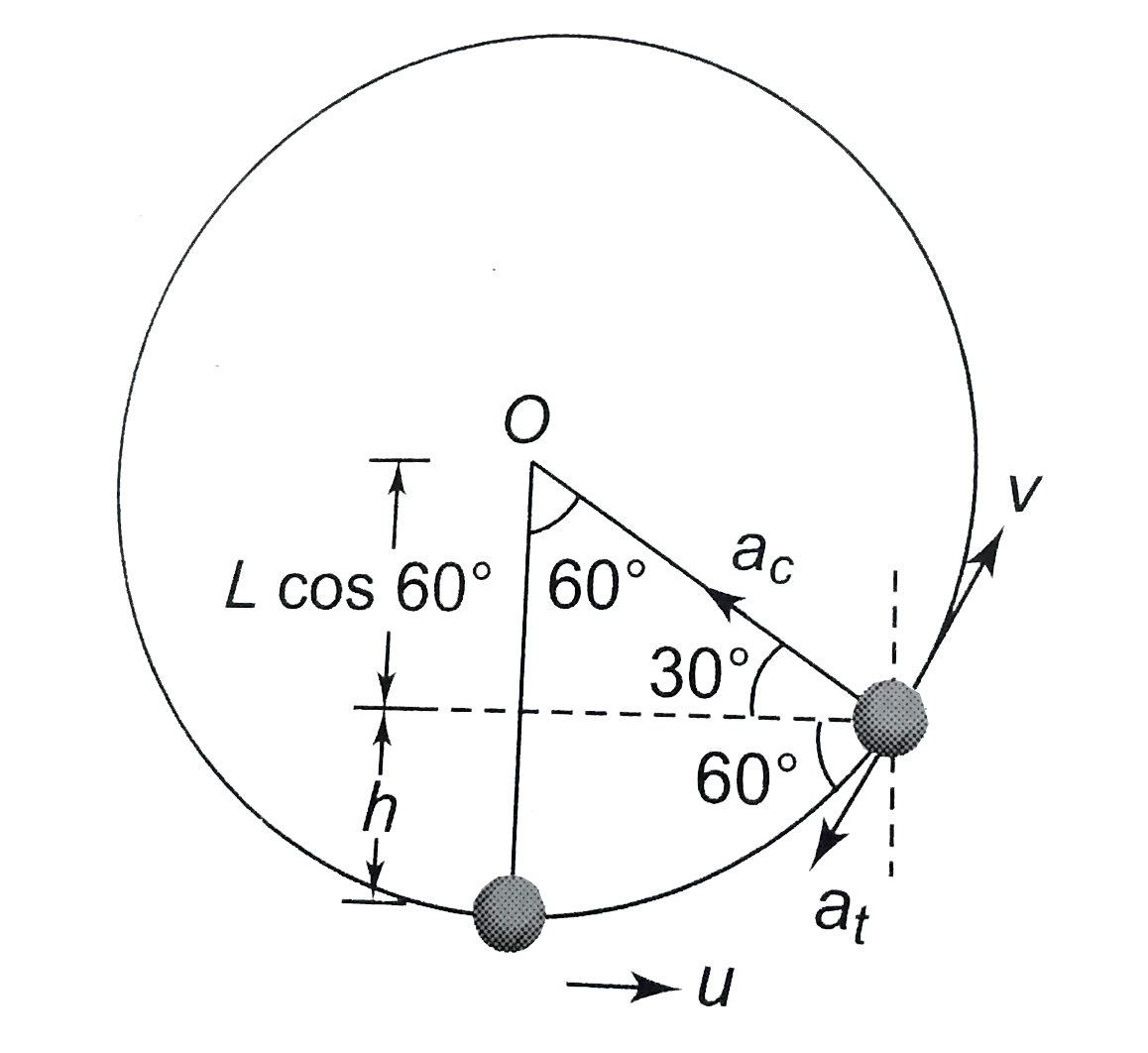
Consider the situation as shown in the figure. The ball attached to a string is moving in the verticle circle find the (a) centripetal acceleration and (b) tanfential acceleration when the string makes an anhle 60∘ with lower vertical. Also, express the total acceleration in vector from taking A as origin.
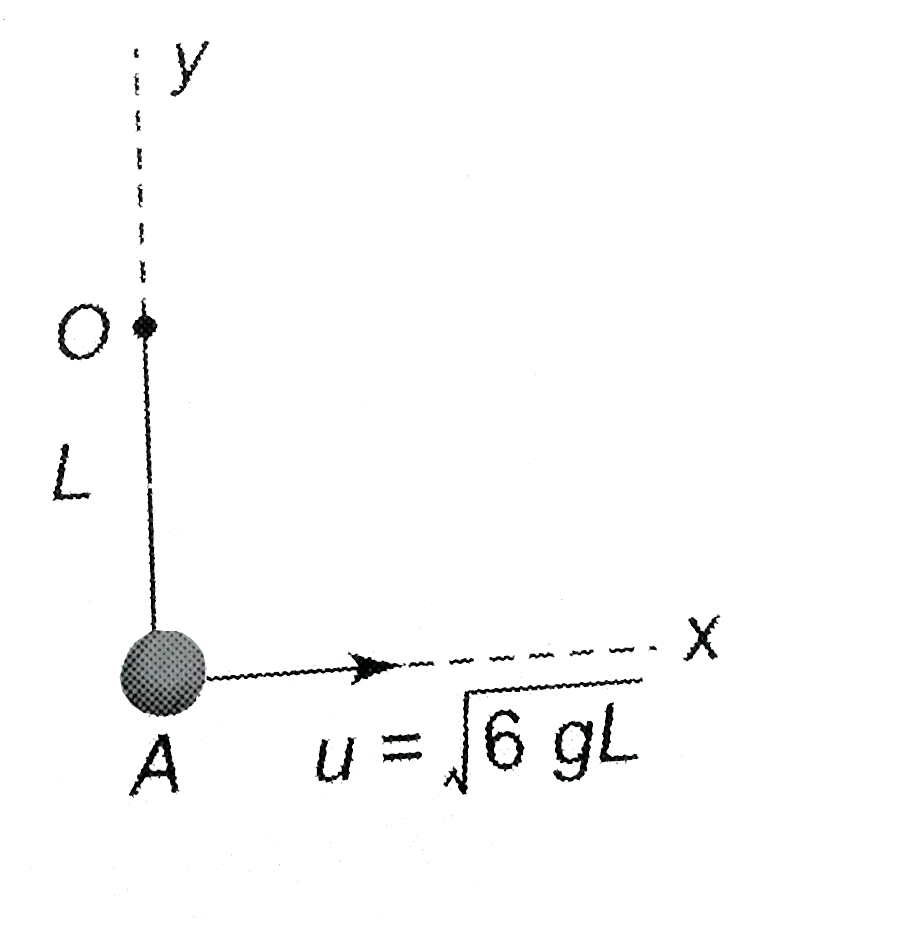
h=L−Lcos60∘=L2
v2=u2−2gh=6gL−2G(L02=5gL
ac=v2L=5g
ac=v2L=5g
at=gsin60∘=√3g2
→a=axˆi+ayˆj
=−(accos30∘+atcos60∘)ˆi
+(acsin30∘−atsin60∘)ˆj
=−(5g×√32+√3g2.12)ˆi+(5g×12−√3g2√32)ˆj
=−11√3g4ˆi+7g4ˆj
Topper's Solved these Questions
Similar Questions
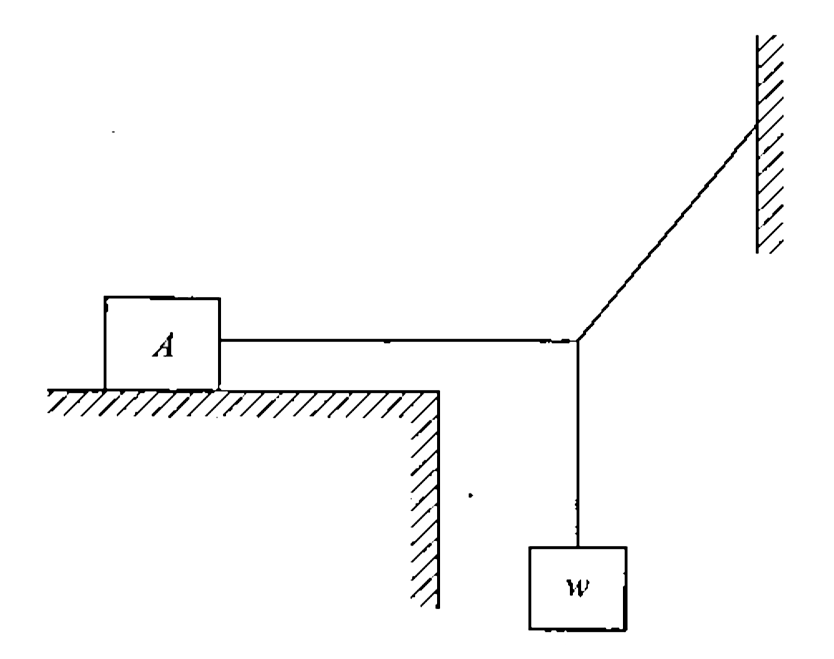
Consider the situation shown in figure. Find the acceleration of the system and the tension in the strings.
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View Solution
Knowledge Check
Consider the situation shown in the figure.
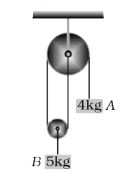
Find acceleration of B.Ag7B2g7C3g7D2g5A body of mass 4 kg is moved in a vertical circle with sufficient speed .Its tangential acceleration , when the string makes an angle of 30∘ with the verticle downward is (g=10mms2)
A4m/sB5m/sC8m/sD7.8m/sA body attached at one end of a string crosses the topmost point of a vertical circle with the critical speed Its centripetal acceleration , when the string is horizontal will be
AgB3gC5gD6g
Consider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

View SolutionConsider the situation shown in figure .Both the pulleys and the string and light and all the surfaces are smooth.
(a) Find the acceleration of 1kg block.
(b) Find the tension in the string. (g=10m/s2).

View SolutionConsider the situation shown in figure. Both the pulleys and the strings are light and all the surfaces are frictionless. Calculate
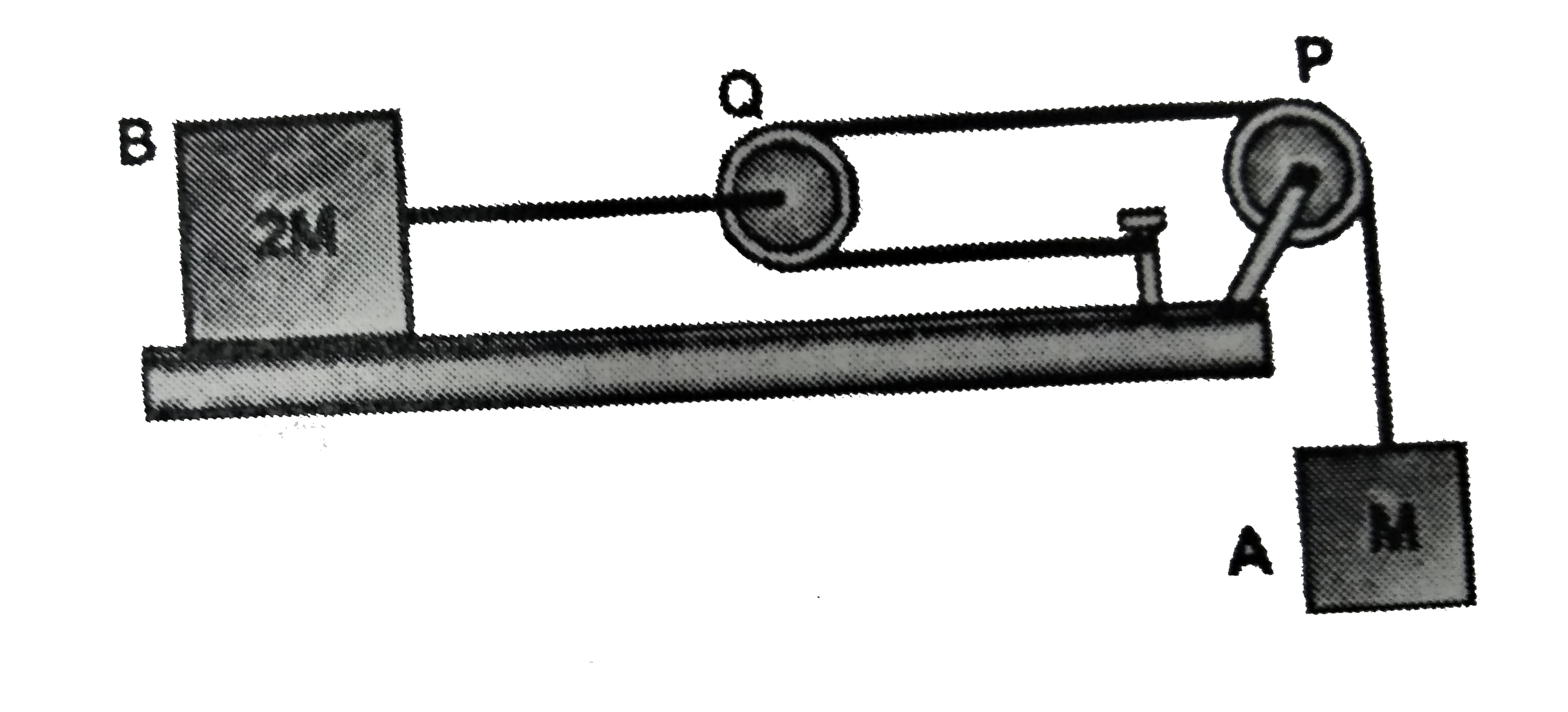
(a) the acceleration of mass M,
(b) tension in the string PQ and
(c ) force exerted by the pulley P.
View SolutionA body crosses the topmost point of a vertical circle with a critical speed. Its centripetal acceleration, when the string is horizontal will be
View SolutionA mass attached to one end of a string crosses top - most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be
(where, g=gravitational acceleration)
View Solution