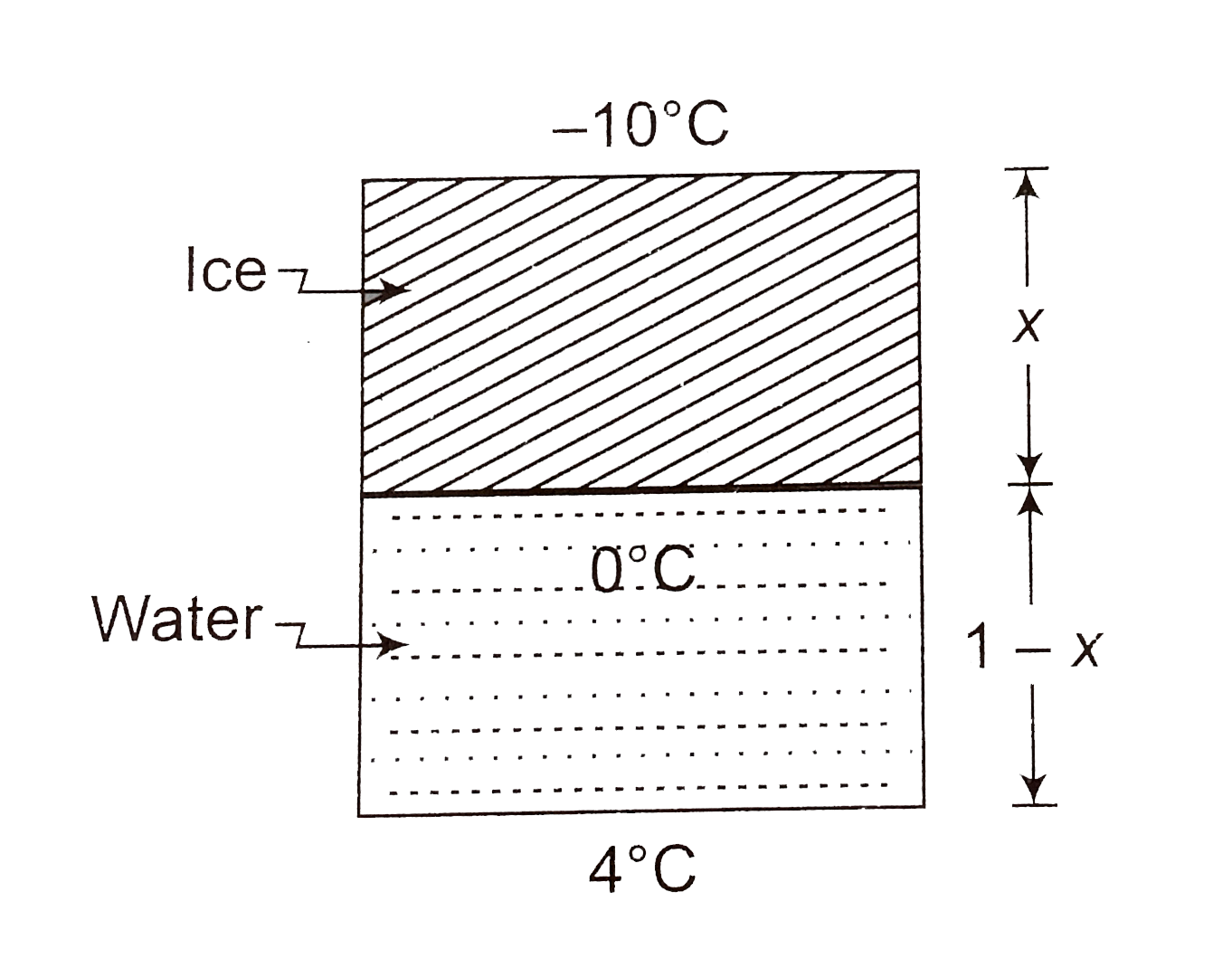
Consider the situation of the previous problem. Assume that the temperature of the water at the botton of the lake remains constant at $4^{\circ} C$ as the ice forms on the surface (the heat required to maintain the temperature of the bottom layer may come from the bed of the lake). The depth of the lake is $1.0 m$ . Show that the thickness of the ice formed attains a steady state maximum value. Find this value. The thermal conductivity of water $= 0.50 W m^{- 1} .^{\circ} C^{- 1}$ . Take other relevent data form the previous problelm.

Video Solution

Text Solution

Verified by Experts

When heat current in water and ice is same, steady state is reached
$i = \frac{4 - 0}{R_{w}} = \frac{0 - (- 10)}{R_{i c e}}$
$4 R_{i c e} = 10 R_{w}$
$4 \frac{x}{K_{i c e} A} = 10 \frac{(1 - x)}{K_{w} A}$
$\frac{4 x}{1.7} = \frac{10 - 10 x}{0.5}$
$2 x = 17 - 17 x$
$x = \frac{17}{19} m = 0.89 m$

Updated on:21/07/2023

The temperature of water at the bottom of a lake whose upper surface has frozen to ice would be around
A $- 10^{\circ} C$
B $0^{\circ} C$
C $4^{\circ} C$
D $- 4^{\circ} C$
Surface water of a lake is about to freeze. What will be the temperature (in °C) of water at the bottom of the lake?
A0
B $- 1$
C1
D4
The top of a lake is frozen as the atmospheric temperature is $- 10^{\circ} C$ . The temperature at the bottom of the lake is most likely to be,
A $4^{\circ} C$
B $0^{\circ} C$
C $- 4^{\circ} C$
D $- 10^{\circ} C$