Consider the situation of the previous question from a frame moving with a speed v0 parallel to the initial velocity of the block? b. What is the work done by the kinetic friction?
To solve the problem, we need to analyze the work done by kinetic friction from a frame moving with a speed v0 parallel to the initial velocity of the block.
1. Identify the Initial and Final Velocities:
- In the original frame, the block has an initial velocity v0 and it comes to a stop after traveling a distance L.
- In the moving frame (which is also moving with speed v0), the initial velocity of the block relative to this frame is 0 (since both the block and the frame are moving at the same speed).
- The final velocity of the block in this frame is also v0 (the block stops, but the frame continues to move).
2. Calculate the Initial and Final Kinetic Energies:
- The initial kinetic energy KEi in the moving frame is:
KEi=12m(0)2=0
- The final kinetic energy KEf in the moving frame is:
KEf=12m(v0)2
3. Determine the Work Done by Kinetic Friction:
- The work done by the kinetic friction W can be calculated using the change in kinetic energy:
W=KEf−KEi
- Substituting the values we found:
W=12m(v0)2−0=12m(v0)2
4. Conclusion:
- The work done by the kinetic friction in this frame is positive and equals:
W=12m(v0)2
- In the original frame, the block has an initial velocity v0 and it comes to a stop after traveling a distance L.
- In the moving frame (which is also moving with speed v0), the initial velocity of the block relative to this frame is 0 (since both the block and the frame are moving at the same speed).
- The final velocity of the block in this frame is also v0 (the block stops, but the frame continues to move).
- The initial kinetic energy KEi in the moving frame is:
KEi=12m(0)2=0
- The final kinetic energy KEf in the moving frame is:
KEf=12m(v0)2
- The work done by the kinetic friction W can be calculated using the change in kinetic energy:
W=KEf−KEi
- Substituting the values we found:
W=12m(v0)2−0=12m(v0)2
- The work done by the kinetic friction in this frame is positive and equals:
W=12m(v0)2
Topper's Solved these Questions
Similar Questions
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. A. What are the initial and final kinetic energies of the ball? b. What is the work done by the kinetic friction?
View SolutionA 100 kg block is started with a speed of 2.0ms−1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) consider the situation from a frame of reference moving at 2.0ms−1 along the initial velocity of the block. as seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at 2.0ms−1, calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c ) find the work done in this frame by the external force holding the belt.
View Solution
Knowledge Check
A block of mass 2kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between the block and surface is 0.1. the work done by friction in 10 s is
A200JB−200JC600 JD−600J
In the previous illustration. Consider the situation when the string is completely compressed. Then it begins to relax and will come to its original length.
a. What is the work done by the spring during the period?
b. Is the work done by the spring positive or negative?
View SolutionConsider the situation of the previous problem. Consider the fastest electron emitted parallel to the large metal plate. Find the displacement of this electron parallel to its initial velocity before it strikes the large metal plate.
View SolutionTwo blocks A and B of mass m and 2m respectively are moving towards a massive (mass>>2m) cliff with velocities 2v and v respectively. The cliff moves with a velocity v. If the coefficient of restitution of collision at the surface of the cliff is e=1/2, find the:

a. velocity of the block B just after colliding with the cliff.
b. work done by the cliff during collision.
c. maximum compression of the spring of stiffness k which is fitted with the block B.
View SolutionA block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces an acceleration F2(m+M) in the sytem. The two blocks always move together. Consider displacement d of the system.
a. Find the work done by friction on bigger block.
b. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.
c. Find the frictional acting on the smaller block.
d. Find the work done by the force of friction on the smaller block by the bigger block.
e. Find the work done by static friction on bigger block.
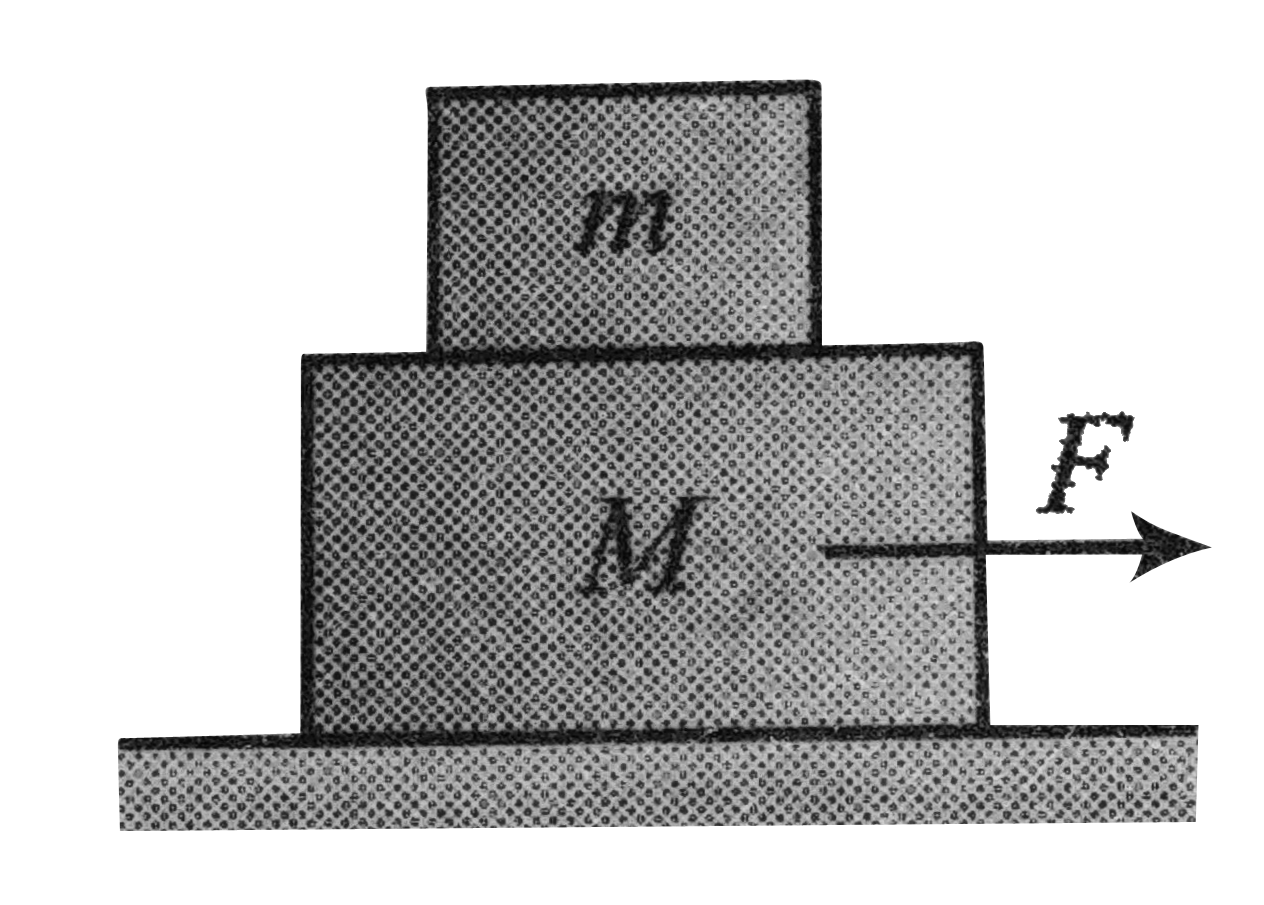
View SolutionA small block of mass m is kept on a rough inclined surface of inclination θ fixed in a car. The car moves with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
_PHY_E05_250_Q01.png)
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
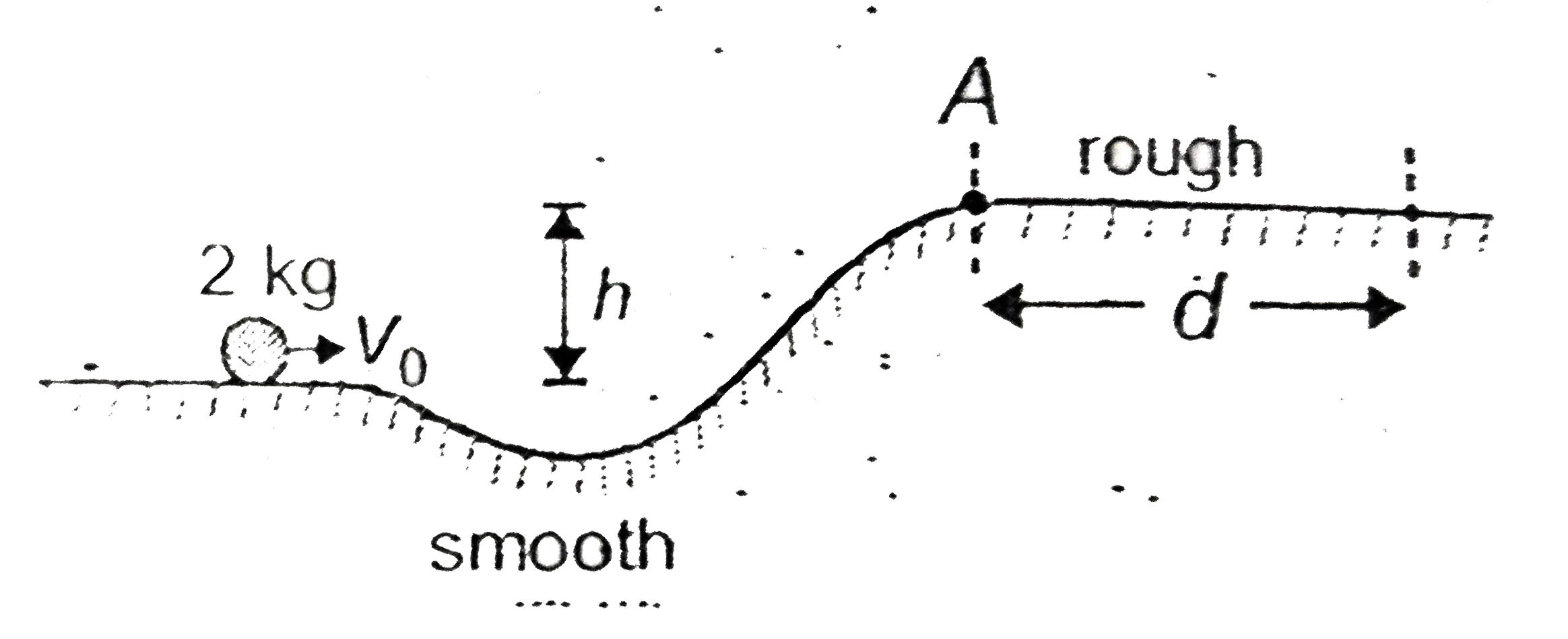
What is the work done by friction force on the body during the motion.
View Solution
