Consider the situation shown in . The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separted by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangualr region and a resistance R connects the rails outsided the field region At t= 0, the wire PQ is puched towards right with a speed v0. find (a) the current in the loop at an instant when the speed of the wire PQ is v, (b) the acceleration of the wire at this instatn, (c ) the velocity v as a function of x and (d) the maximum distance the wire will move.
 Solution in Gujrati
Solution in Gujrati
(a) When the speed is v <br>emf=B/v,<br>Resistance= r+R<br>:. Current = (Blv)/(r+R)V<br>(b) Force acting on the wire =i//B<br>=(BlvlB)/(R+r)=(B^2l^2v)/(R+r))<br> Acceleration on the wire<br><br>(c ) v=v_0+at=v_0-(B^2l^2v)/(R+r))t<br> [Force is opposite to velocity ]<br>v_0-(B^2l^2v)/(R+r))<br> (d) a=v(dv)/(dx)=(B^2l^2v)/(R+r))<br> dx= (dvm(R+r))/(B^2l^2)<br>x=(m(R+r))/(B^2l^2).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA rod of mass m , length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v . If a uniform horizontal magnetic field B exists, then find thevalue of B .
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
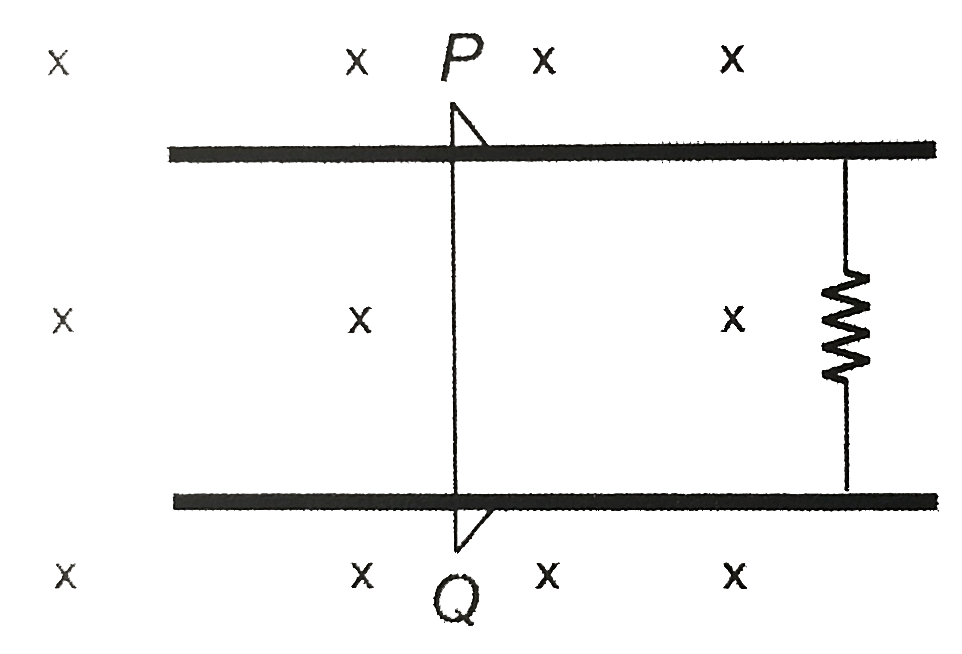
View SolutionConsider the situation shown in the figure. The wire PQ has mass m , resistance r and can slide 0n the smooth, horizontal parallel rails separated by a distance l . The resistance of the rais is negiligible. A uniform magnetic field B exists in the reactangular region and a resistance R connects the rail outside the field region. At t=0 , the wire PQ is pushed toward right with a speed v0 . Find
(a) the current in the loop at an instant when the speed of the wire PQ is v
(b) the acceleration of the wire as this instant
(c) the velocity v as a function of x
(d) the maximum distance the wire will move
(e) the velocity as a function of time
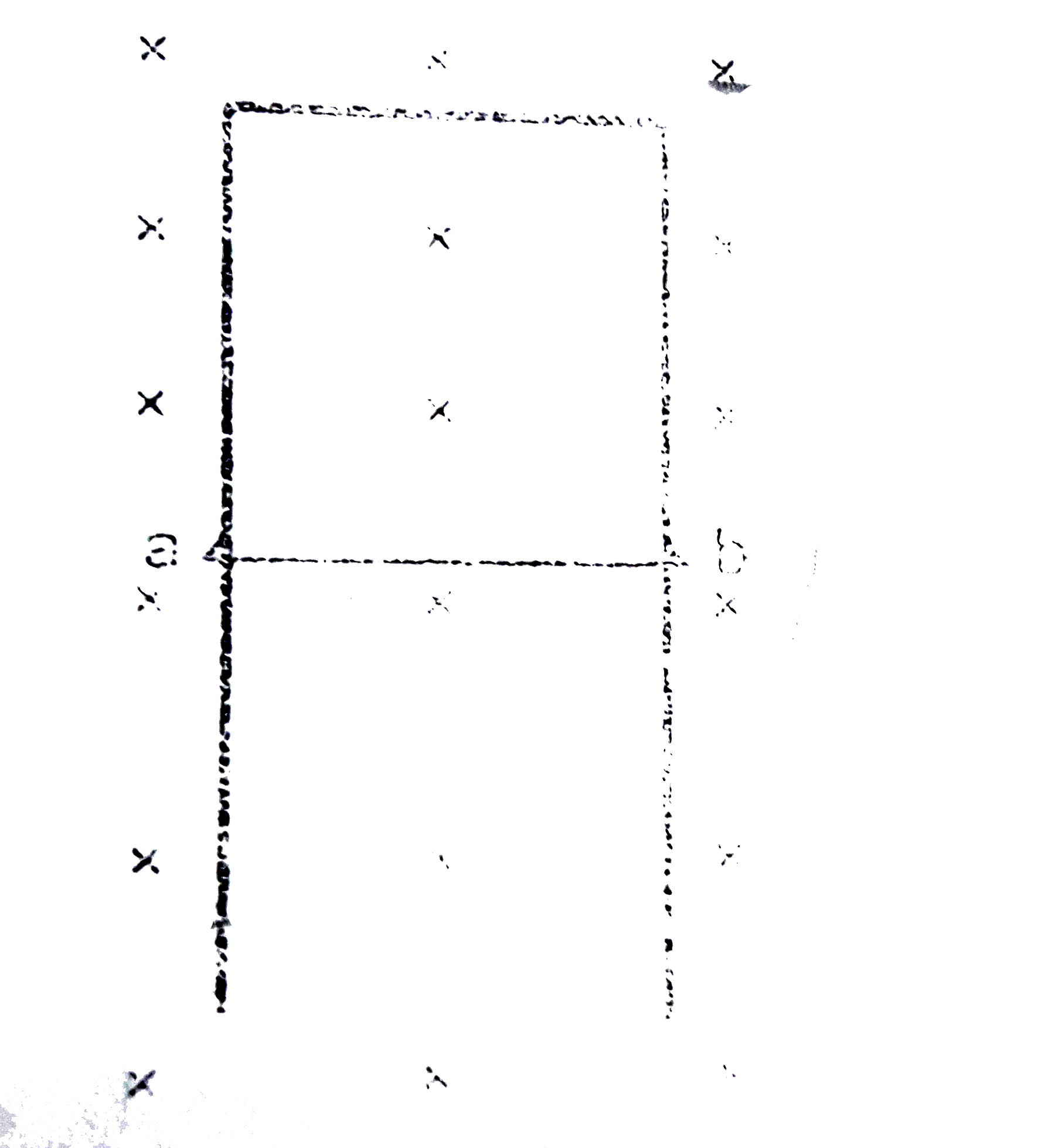
View SolutionA copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
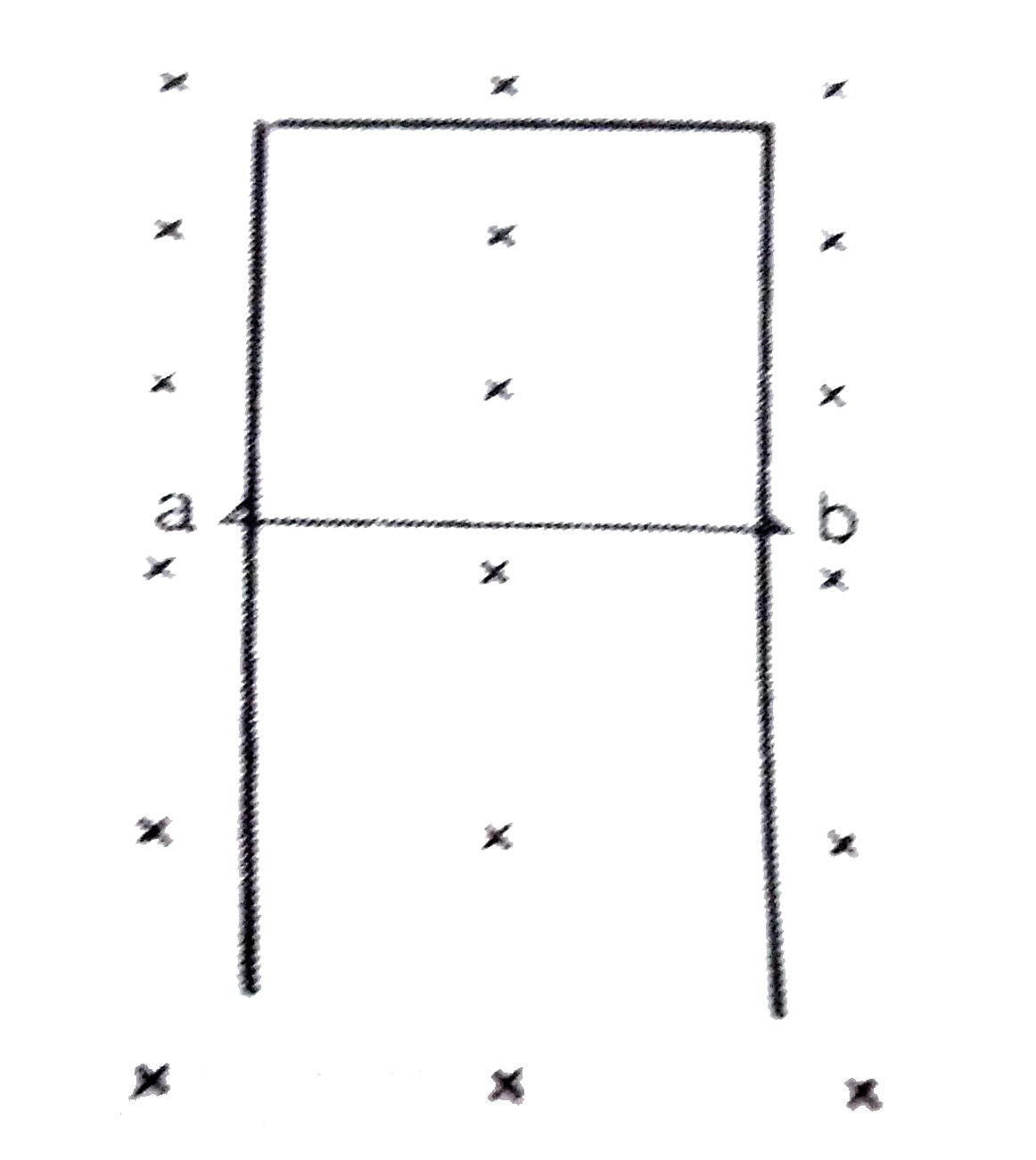
View SolutionA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View Solutionएक कॉपर की छड़ का द्रव्यमान m है। यह दो क्षैतिज समान्तर चिकनी पटरियों (rails) जिनके बीच की दूरी । है तथा क्षैतिज के साथ θ कोण बनाती है, पर गुरुत्व के अन्तर्गत फिसलती है। तली में पटरियाँ एक प्रतिरोध R के द्वारा चित्रानुसार जुड़ी हैं। यहाँ एकसमान चुम्बकीय क्षेत्र B पटरियों (rails) के तल के लम्बवत् है। छड़ का क्रान्तिक वेग है

View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
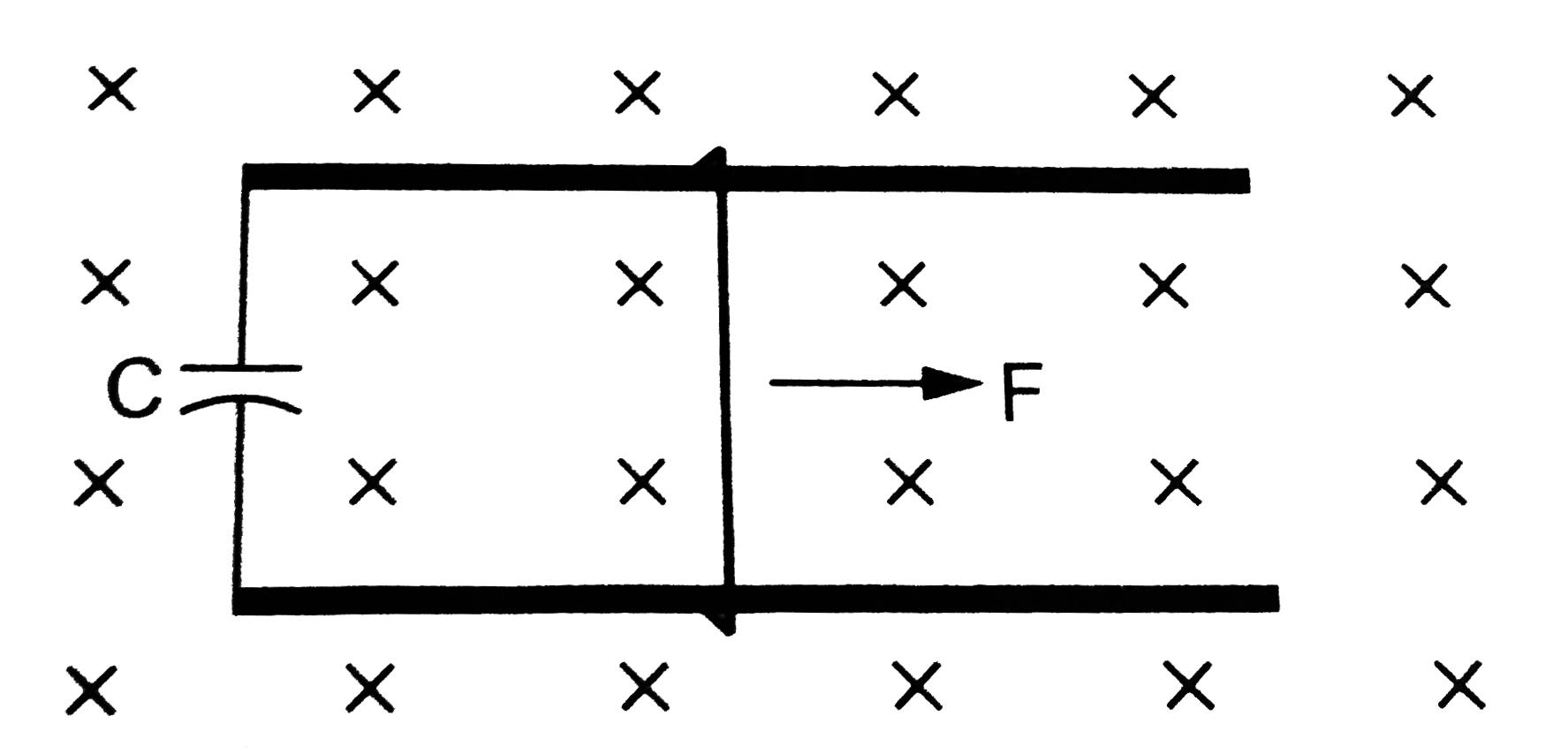
View SolutionConsider the situation shown in . The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separted by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangualr region and a resistance R connects the rails outsided the field region At t= 0, the wire PQ is puched towards right with a speed v0. find (a) the current in the loop at an instant when the speed of the wire PQ is v, (b) the acceleration of the wire at this instatn, (c ) the velocity v as a function of x and (d) the maximum distance the wire will move.

View SolutionA rod of mass m , length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v . If a uniform horizontal magnetic field B exists, then find thevalue of B .
View SolutionConsider the situation shown in . The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separted by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangualr region and a resistance R connects the rails outsided the field region At t= 0, the wire PQ is puched towards right with a speed v0. find (a) the current in the loop at an instant when the speed of the wire PQ is v, (b) the acceleration of the wire at this instatn, (c ) the velocity v as a function of x and (d) the maximum distance the wire will move.
(##HCV_VOL2_C38_E01_073_Q01##)
View Solution
