Consider two cities P and Q between which consistent bus servece is available in both directions every x mimutes. A morning jogger is jogging towards Q from P wigh a speed of 10kmh−1. Every 18mim a bus crosses this jogger in its own direction of motion and every 6min another bus crosses in opposite direction. What is time preriod between two consecutive buses and also find the speed of buses ?.
To solve the problem, we need to find the time period between two consecutive buses (denoted as x) and the speed of the buses (denoted as V). Let's break down the solution step by step.
Step 1: Define the Variables
- Speed of the jogger, Vj=10 km/h
- Speed of the bus, V km/h
- Time interval between buses, x minutes
Step 2: Convert Time to Hours
Since the speeds are given in km/h, we should convert the time intervals from minutes to hours:
- 18 minutes = 1860=0.3 hours
- 6 minutes = 660=0.1 hours
Step 3: Relative Speed in the Same Direction
When a bus is moving in the same direction as the jogger, the relative speed of the bus with respect to the jogger is:
V−Vj=V−10 km/h
Using the formula for distance (Distance = Speed × Time), the distance covered by the bus in the time it takes to cross the jogger is:
Distance=(V−10)×0.3
Since the distance between two buses is also given by:
Distance=V×x60
Setting these equal gives us:
(V−10)×0.3=V×x60
Multiplying both sides by 60 to eliminate the fraction:
18(V−10)=Vx
This simplifies to:
18V−180=Vx
(Equation 1)
Step 4: Relative Speed in the Opposite Direction
When a bus is moving in the opposite direction to the jogger, the relative speed is:
V+Vj=V+10 km/h
The distance covered by the bus in this case is:
Distance=(V+10)×0.1
Setting this equal to the distance between buses:
(V+10)×0.1=V×x60
Multiplying both sides by 60:
6(V+10)=Vx
This simplifies to:
6V+60=Vx
(Equation 2)
Step 5: Solve the Equations
Now we have two equations:
1. 18V−180=Vx
2. 6V+60=Vx
Setting them equal to each other:
18V−180=6V+60
Rearranging gives:
18V−6V=60+180
12V=240
V=20 km/h
Step 6: Find the Time Interval x
Now, substitute V=20 km/h back into either Equation 1 or Equation 2 to find x. Using Equation 2:
6(20)+60=20x
120+60=20x
180=20x
x=9 minutes
Final Answer
- The speed of the buses is 20 km/h.
- The time period between two consecutive buses is 9 minutes.
- Speed of the jogger, Vj=10 km/h
- Speed of the bus, V km/h
- Time interval between buses, x minutes
Since the speeds are given in km/h, we should convert the time intervals from minutes to hours:
- 18 minutes = 1860=0.3 hours
- 6 minutes = 660=0.1 hours
When a bus is moving in the same direction as the jogger, the relative speed of the bus with respect to the jogger is:
V−Vj=V−10 km/h
Using the formula for distance (Distance = Speed × Time), the distance covered by the bus in the time it takes to cross the jogger is:
Distance=(V−10)×0.3
Distance=V×x60
Setting these equal gives us:
(V−10)×0.3=V×x60
Multiplying both sides by 60 to eliminate the fraction:
18(V−10)=Vx
This simplifies to:
18V−180=Vx
(Equation 1)
When a bus is moving in the opposite direction to the jogger, the relative speed is:
V+Vj=V+10 km/h
The distance covered by the bus in this case is:
Distance=(V+10)×0.1
Setting this equal to the distance between buses:
(V+10)×0.1=V×x60
Multiplying both sides by 60:
6(V+10)=Vx
This simplifies to:
6V+60=Vx
(Equation 2)
Now we have two equations:
1. 18V−180=Vx
2. 6V+60=Vx
18V−180=6V+60
Rearranging gives:
18V−6V=60+180
12V=240
V=20 km/h
Now, substitute V=20 km/h back into either Equation 1 or Equation 2 to find x. Using Equation 2:
6(20)+60=20x
120+60=20x
180=20x
x=9 minutes
- The speed of the buses is 20 km/h.
- The time period between two consecutive buses is 9 minutes.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.416videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.212videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T min. A man cycling with a speed of 20kmh−1 in the direction A to B notices that a bus goes past him every 18min in the direction of his motion, and every 6min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant )do the buses ply on the road?
View SolutionA : According to Newton's third law of motion for every action, there is an equal and opposite reaction.
R : There is no time lag between action and reaction.View Solution
Knowledge Check
- Question 1 - Select One
Two town A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man leaving in either direction every in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. The period T of the bus service is
A4.5 minB9 minC1.2 minD24 min - Question 2 - Select One
Two particles execute SHMs of the same amplitude and frequency along the same straight line. They cross one another when going in opposite direction. What is the phase difference between them when their displacements are half of their amplitudes ?
A60∘B30∘C120∘D150∘ - Question 3 - Select One
Two trains, each 50 m long are travelling in opposite direction with velocity 10 m/s and 15 m/s. The time of crossing is
A2sB4sC2√3sD4√3 s
If current in two parallel wires flow in opposite directions, the force between the wires will:
View SolutionThe equivalent capacitance between P and Q in the figure is (area of each plate is A and separation between two consecutive plates is d)
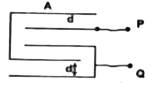 View Solution
View SolutionTwo cities AandB are connected by a regular bus service with buses plying in either direction every T seconds. The speed of each bus is uniform and equal to Vb. A cyclist cycles from A→B with a uniform speed of Vc. A bus goes past the cyclist in T1 second in the direction A→B and every T2 second in the direction B→A. Then
View SolutionWhat is the speed of a photon with respect to another photon if (a) the two photons are going in the same direction and (b) they are going in opposite directions?
View SolutionTwo cars get closer by 8 m every second while traveling in the opposite directions. They get closer by 0.8 m while traveling in the same directions. What are the speeds of the two cars ?
View Solution

