Consider two sources A and B as shown in the figure below . Let the two sources emit simple harmonic waves of same frequency but of different amplitudes , and both are in phase (same phase) . Let O be any point equidistant from A and B as shown in the figure . Calculate the intensity at points O , Y and X . ( X and Y are not equidistant from A & B) Solution in Tamil

The distance between OA and OB are the same and hence , the waves starting from A and B reach O after covering equal distances (equal path lengths) . Thus , the path difference between two waves at O is zero .
OA−OB=0
Since the waves are in the same phase , at the point O , the phase difference between two waves is also zero . thus ,the resultant intensity at the point O is maximum . Consider a point Y , such that the path difference between two waves is λ . Then the phase difference at Y is
Δϕ=2πλ×Δr=2πλ×λ=2π
Therefore , at the point YH , the two waves from A and B are in phase , hence the intensity will be maximum .
Consider a point X , and let the path difference the between two waves be λ2 . Then the phase difference at X is
Δϕ=2πλλ2=π
Therefore , at the point X , the wave meet and are in out of phase . Hence , due to destructive interference , the intensity will be maximum .
Topper's Solved these Questions
- BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Textual Evaluation Solved (Multiple Choice Questions )15videos
WAVES
- BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Textual Evaluation Solved (Short Answer Questions )15videos
WAVES
- BOOK - FULL MARKSCHAPTER - SOLVED PAPER 17 (UNSOLVED)EXERCISE - Part-IV10videos
SOLVED PAPER 17 (UNSOLVED)
- BOOK - FULL MARKSCHAPTER - WORK, ENERGY AND POWEREXERCISE - Additional Question Solved (Numercials)11videos
WORK, ENERGY AND POWER
Similar Questions
A student tunes his guitar by striking a 120 Hertz with a tuning fork, and simultaneously plays the 4th string on his guitar. By keen observation, he hears the amplitude of the combined sound oscillating thrice per second. Which of the following frequency is the most likely the frequency of the 4th string on his guitar ?
04:50View SolutionWhat is meant by waves?
04:01View SolutionIn a series of successive measurements in an experiment, the readings of the period of oscillation of a simple pendulum were found to be 2.63s, 2.56s, 2.42, 2.71s and 2.80 s. Calculate
(i) the mean value of the period of oscillation
(ii) the absolute error in eah measurement
(iii) The men absolute error (iv) the relative error (v) the percentage error. Expresss the results in proper form.03:41View SolutionA body is moving along z-axis of a coordinate system under the effect of a constant force F=(2→i+3ˆj+vˆk)N. Find the work done by the force in moving the body a distance of 2 m along z-axis
05:31View SolutionFind the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
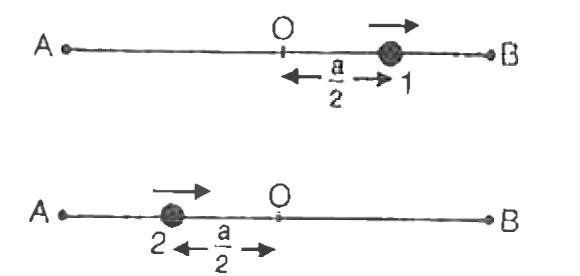 View Solution
View SolutionTwo waves of same frequency and same amplitude from two monochromatic sources are allowed to superpose at a certain point. If in one case the phase difference is 0 and in other case it is π/2 then the ratio of the intensities in the two cases will be
View SolutionWaves from two different sources overlap near a particular point. The amplitude and the frequency of the two waves are the same.The ratio of the intensity,when the two waves arrives in the phase to that when they arrive 90∘ out of phase is
05:13View SolutionThe frequencies of sources A and B as shown in figure are same. The nature of interference at points P, Q and R will be if AB = (lambda)/(2) and the two sources are in same phase.
05:13View SolutionWaves from two different sources overlap a particular point. The amplitude and frequency of the two waves are same.The ratio of the intensity when the two waves arrive in phase to that when they arrive 90∘ out of phase is :
View SolutionWaves from two different sources overlap near a particular point. The amplitude and the frequency of the two waves are same. The ratio of the intensity when the two waves arrive in phase to that when they arrive 90∘ out phase is
03:33View SolutionWaves of same amplitude and same frequency from two coherent source overlap at a point. The ratio of the resultant intensity when they arrive in phase to that when they arrive with 90∘ phase difference is
06:18View SolutionWaves of same amplitude and same frequency from two coherent source overlap at a point. The ratio of the resultant intensity when they arrive in phase to that when they arrive with 90∘ phase difference is
View SolutionWaves of same amplitude and same frequency from two coherent sources overlap at a point. The intensity when they arrive in phase to that when they arrive with90∘ phase difference is
03:38View SolutionWaves from two different sources overlap near a particular point. The amplitude and the frequency of the two waves are the same.The ratio of the intensity,when the two waves arrives in the phase to that when they arrive 90^(@) out of phase is
03:21View SolutionTwo sources of sound are separated by a distance 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180∘ out of phase. At what points between the two sources, will the sound intensity be maximum?
02:00View Solution

