Corresponding to displacement equation,
y=Asin(kx+ωt)
of a longitudinal wave make its pressure and density wave also. Bulk modulus of the medium is B and density is p.
The correct Answer is:A, B, C, D
Give, y(x,t)=Asin(kx+ωt)
∂y∂x=kAcos(kx+ωt) ..(i)
Now, pressure equation is given by
Δp=−B(∂y∂x)
subsituting the value of ∂y∂x from Eq. (i) we have
Δp=−BAkcos(kx+ωt)
Similarly, density equation is give by
(Δp)=ρB(Δp)=ρB(−B∂y∂x)=−ρ(∂y∂x)
substituting the value of ∂y∂x from Eq. (i), we have,
Δρ=−ρAkcos(kx+ωt)
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Example Type 1
4 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Example Type 2
2 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
The equation y=Asin2(kx−ωt) represents a wave motion with
View SolutionIn a wave motion y=asin(kx−ωt), y can represent
View Solution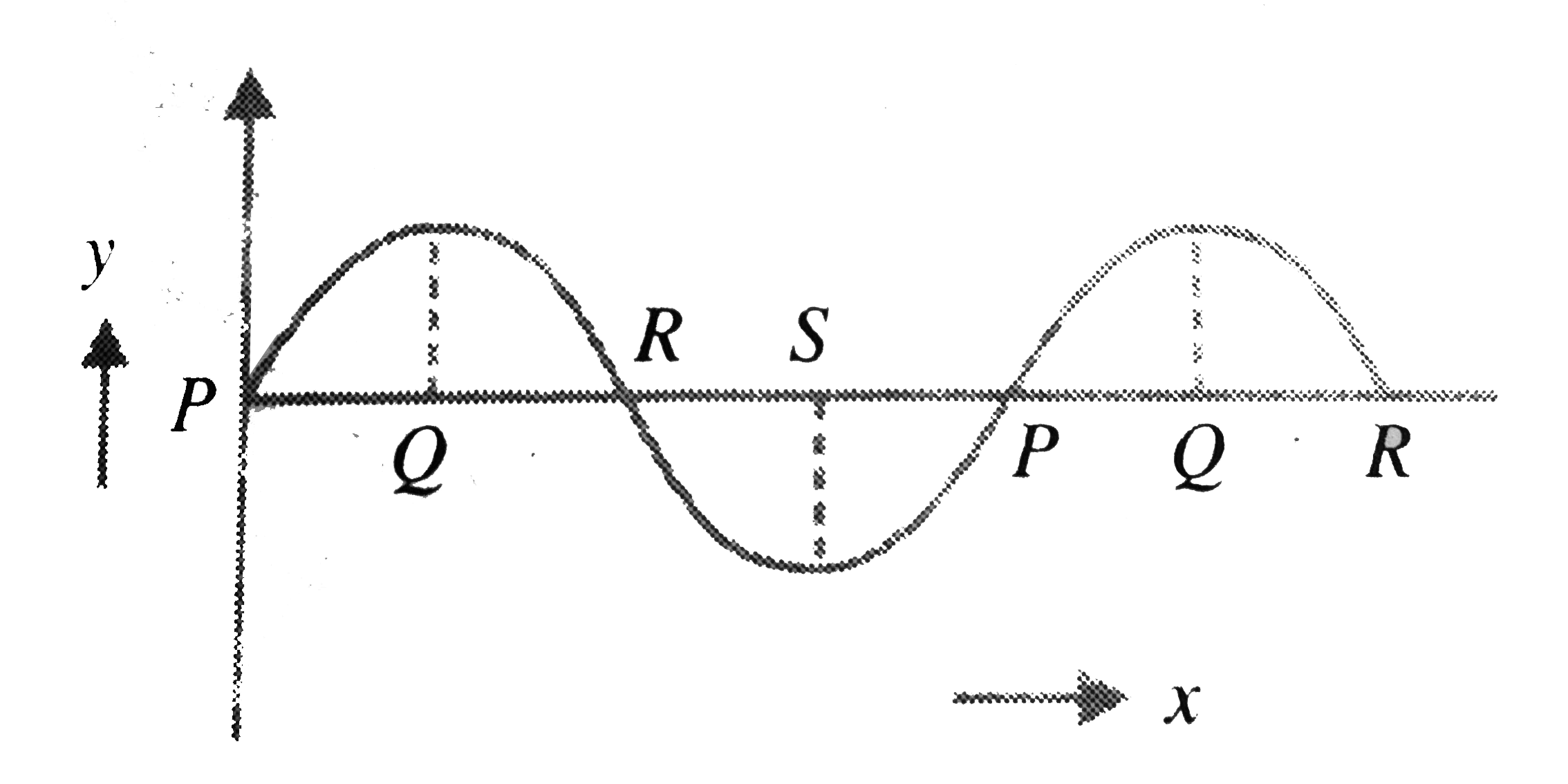
Figure. Represents the displacement y versus distance x along the direction of propagation of a longitudinal wave. The pressure is maximum at position marked
View SolutionThe equation y= A sin2(ωt - kx) represent a wave motion with amplitude and frequency as
View SolutionProve that the equation y=asinωt does not satisfy the wave equation and hence it does not represent a wave.
View SolutionA sinusoidal wave is given by y=A sin (kx-ωt). The ratio of its maximum particle velocity to wave velocity is
View SolutionCalculate the speed of longitudinal sound wave in a liquid. The bulk modulus for the liquid is 20×109N/m2 and its density is 9.5×103kg/m3.
View SolutionIf the speed of longitudinal mechanical waves in water is 1400m/s then calculate the bulk modulus of elasticity of water. (given density of water is 1g/cm3)
View SolutionIf the speed of longitudinal mechanical waves in water is 1400m/s then calculate the bulk modulus of elasticity of water. (given density of water is 1g/cm3)
View SolutionA travelling wave in a stretched string is described by the equation y=Asin(kx−ωt) the maximum particle velocity is
View Solution
