Deduce an expression for the mutual inductance of two long coaxial solenoids but having different radii and different number of turns.
Or
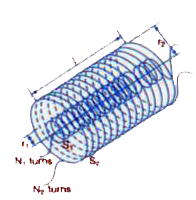
Obtain the expression for the mutual inductance of two long coaxial solenoids S1 and S2 wound one over the other, each of length I and radii r1andr2, and number of turns per unit length n1andn2 respeetively, when a current I is set up in the outer solenoid S2.
Consider two long coaxial solenoids each of length l. Let radius of inner solenoid S1,ber1, for cross section area be A1 and n1 be the number of turns per unit length in it. The corresponding quantities for outer solenoid S1ber1,A2andn2. Total number of turns in two solenoids are N1=n1l and N2=n2l respectively.
Let a current I2, is set up through outer solenoid S2 so that magnetic field developed along its axial line
B=μ0n0I2
∴ Magnetic flux linked per unit turn of solenoid coil S1,ϕ1=BA1=μ0n2I2A1
and total magnetic flux linked with solenoid S1,N1ϕ1=N1μ0n2A1I2=μn1n2l.πr21I2
As per definition of mutual inductance Nϕ1=M2I2
∴ mu_(0)n_(1)n_(2)l.pir_(1)^(2)I^(2)<br>implies M_(12) = mu_(0)n_(1)n_(2)l.pir_(1)^(2) = mu_(0)n_(1)n_(2)lA_(1) = (mu_(0)N_(1)N_(2)A_(1))/l<br>Forapairoftwoso≤nooilsM_(12) = M_(21) = M,henceμtual∈ductanceofpairofso≤nooilis<br>M = mu_(0)n_(1)n_(2)l.pir_(1)^(2) = (mu_(0)N_(1)N_(2)A_(1))/l<br>Ifasoftironcoreofrelativepermeabilitymu_(r),isalso∈sertedS_(1),turns∈stheso≤nooilS,theμtual∈ductancebecomes<br>M = mu_(0)n_(1)n_(2)l pir_(1)^(2) = (mu_(0)N_(1)N_(2)A_(1))/l
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Long Answer Questions -I16videos
ELECTROMAGNETICE INDUCTION
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Long Answer Questions -II9videos
ELECTROMAGNETICE INDUCTION
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Very Short Answer Questions30videos
ELECTROMAGNETICE INDUCTION
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)1videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST1videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
Similar Questions
Define mutual inductance between two long coaxial solenoids. Find out the expression for the mutual inductance of inner solenoid of length l having the radius r1 and the number of turns n1 per unit length due to the second other solenoid of same length and n2 number of turns per unit length.
View SolutionDefine mutual inductance between a pair of coils. Derive expression for the mutual inductance of two long coaxial solenoids of same length wound one over the other.
View SolutionDefine the term 'mutual inductance between the two coils. Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1andr2(r2>r1). Total number of turns in two solenoids are N1andN2 respectively.
View SolutionThere are two long co-axial solenoids of same length l. The inner and other coils have redii r1 and r2 and number of turns per unti length n1 and n2 respectively .The reatio of mutual inductance to the self - inductance of the inner- coil is :
View SolutionThere are two long co-axial solenoids of same length l. The inner and other coils have redii r1 and r2 and number of turns per unti length n1 and n2 respectively .The reatio of mutual inductance to the self - inductance of the inner- coil is :
View SolutionDefine the term 'mutual inductance' between the two coils.
Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of I and radii r1andr_(2)(r_(2)gt gt r_(1)).Totalνmberofso≤noareN_(1) and N_(2) respectively.View SolutionFind the mutual inductance of two long concentric solenoids for a length I. The area of cross-section of inner solenoid is A and number of turns per unit length are n1 and n2.
View SolutionFind the mutual inductance of two long concentric solenoids for a length l. The area of cross-section of inner solenoid is A and number of turns per unit length are n1 and n2.
 View Solution
View SolutionDerive the expression for the self inductance of a long solenoid of cross sectional area A and length l, having n turns per unit length.
View SolutionDefine mutual inductance between two long coaxial solenoids. Find out the expression for the mutual of inner solenoid of length 1 having the radius r1 and the number of turns n1 per unit length due to the second other solenoid of same length and n2 number of turns per unit length.
View Solution

