Define angle of friction, angle of repose and obtain the relation for angle of repose (ie., θg=tan−1μ).
Step-by-Step Solution
1. Definitions:
- Angle of Friction (θ): The angle of friction is defined as the angle between the direction of the resultant force of friction and the normal reaction force. It represents the maximum angle at which a body can remain at rest on a surface without sliding.
- Angle of Repose (θ_r): The angle of repose is the minimum angle of inclination of a plane with the horizontal at which a body placed on it just begins to slide down. It is the angle at which the force of static friction is maximized and balances the component of gravitational force acting down the incline.
2. Understanding Forces:
- Consider a block of mass m resting on an inclined plane making an angle θ with the horizontal.
- The gravitational force acting on the block can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
3. Static Friction:
- The static friction force F acts up the incline and is given by:
F=μsR
where μs is the coefficient of static friction and R is the normal reaction force.
4. Normal Reaction Force:
- The normal reaction force R is equal to the perpendicular component of the weight:
R=mgcosθ
5. Equilibrium Condition:
- For the block to be at rest just before sliding, the force of static friction must equal the component of the gravitational force acting down the incline:
F=mgsinθ
6. Setting Up the Equation:
- From the equilibrium condition, we have:
μsR=mgsinθ
- Substituting R from the earlier equation:
μs(mgcosθ)=mgsinθ
7. Simplifying the Equation:
- Dividing both sides by mg (assuming m≠0):
μscosθ=sinθ
8. Final Relation:
- Rearranging gives:
tanθ=μs
- Therefore, the angle of repose θr can be expressed as:
θr=tan−1(μs)
Final Result
The relation for the angle of repose is:
θr=tan−1(μ)
- Angle of Friction (θ): The angle of friction is defined as the angle between the direction of the resultant force of friction and the normal reaction force. It represents the maximum angle at which a body can remain at rest on a surface without sliding.
- Angle of Repose (θ_r): The angle of repose is the minimum angle of inclination of a plane with the horizontal at which a body placed on it just begins to slide down. It is the angle at which the force of static friction is maximized and balances the component of gravitational force acting down the incline.
- Consider a block of mass m resting on an inclined plane making an angle θ with the horizontal.
- The gravitational force acting on the block can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
- The static friction force F acts up the incline and is given by:
F=μsR
where μs is the coefficient of static friction and R is the normal reaction force.
- The normal reaction force R is equal to the perpendicular component of the weight:
R=mgcosθ
- For the block to be at rest just before sliding, the force of static friction must equal the component of the gravitational force acting down the incline:
F=mgsinθ
- From the equilibrium condition, we have:
μsR=mgsinθ
- Substituting R from the earlier equation:
μs(mgcosθ)=mgsinθ
- Dividing both sides by mg (assuming m≠0):
μscosθ=sinθ
- Rearranging gives:
tanθ=μs
- Therefore, the angle of repose θr can be expressed as:
θr=tan−1(μs)
The relation for the angle of repose is:
θr=tan−1(μ)
Topper's Solved these Questions
- SAMPLE QUESTION PAPER-3 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-C
9 Videos
- SAMPLE QUESTION PAPER-2 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-D
10 Videos
- SELF ASSESSMENT PAPER 01BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECION- D (Answer the following )
6 Videos
Similar Questions
Define angle of dip
View SolutionAngle of Friction and Repose
View SolutionWhat is angle of friction?
View SolutionDefine angle of repose. Is this angle equal to the angle of friction ?
View SolutionDefine the term angle of deviation.
View SolutionWhat is the relation between coefficient of friction and angle of repose ?
View SolutionIn the figure shown, angle of repose is 45∘.Find force of friction, net force and acceleration of the block when
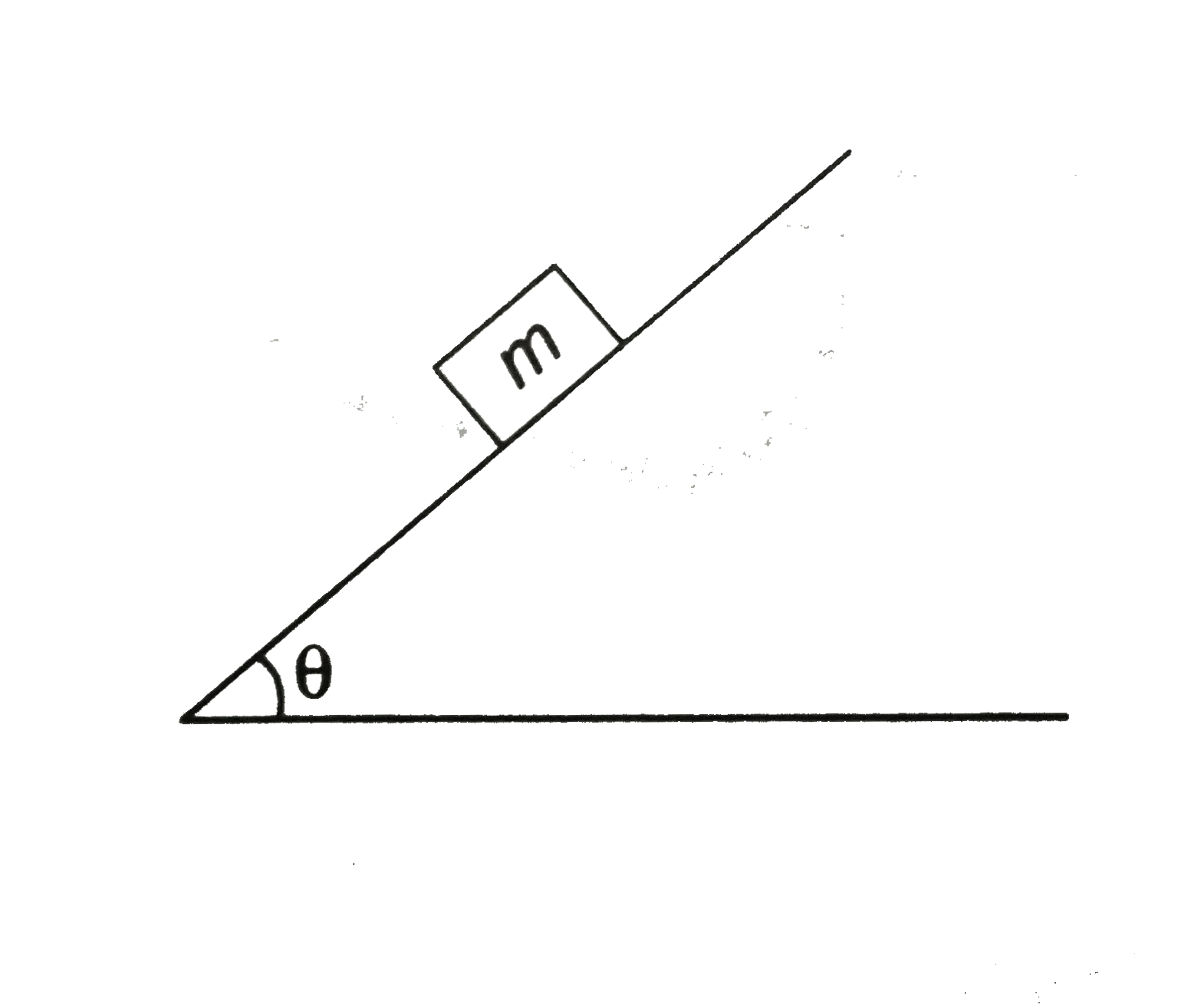
(a) θ=30∘ (b)θ=45∘ (c)θ=60∘
View SolutionMinimum force is needed to move a block on rought surface, if θ= angle of friction.
Angle of friction and angle of repose are numerically same.
View Solution(a) Define the following when refraction takes place through an equilateral glass prism
(i) angle of incidence (ii) prism (iii) refracting angle of prism (iv) angle of emergence (v) angle of deviation
(b) How are angle of incidence, angle of prism, angle of emergence and angle of deviation related to each other?
View SolutionIf the coefficient of friction is √3, the angle of friction is
View Solution