Define electric fied intensity and derive an expression for it at a point on the neuttral axis of a dipole. Also determine its direction.Solution in Punjabi
Electric field intensity at a point is defined as the force experienced by a unit positive charge placed at that point.
In S.I., the unit of E is (NC−1 or Vm−1).
Axial line of an electric dipole is a line joining the centre of two charges and extended on either side. It is also known as End-on-position.
Consider an electric dipole consisting of charges −qand+q, separated by distance 2a and placed in the free space. Let P be a point on the axial line joining the two charges of the dipole at a distance r from the centre O of the dipole.
So OP=r,AP=r+a and BP=r−a
The electric field →E at point P due to dipole will be the resultant of the electric field →EA (due to charge - q at point A) and →EB (due to charge + q at point B) i.e.,
→E=−→EA+−→EB
Now, ∣∣→EA∣∣=14π∈0.qAP2=14π∈0.q(r+a)2 (along PA)
and ∣∣→EB∣∣=14π∈0.qBP2=14π∈0.q(r−a)2 (along PX)
Obviously ∣∣→EB∣∣ is greater than ∣∣→EA∣∣ .
Since →EA and →EB, act along the same line but in opposite direction, the magnitude of the net electric field at point P is given by
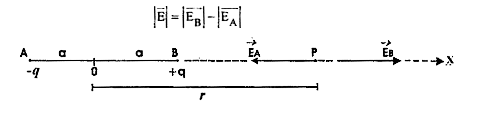
or E=14π∈0.q(r−a)2−14π∈0.q(r+a)2 (along PX)
=14π∈0.q[(r+a)2−(r−a)2(r2−a2)2]
or E=14π∈0.q(4ra)(r2−a2)2=14π∈0q(2a)(2r)(r2−a2)2
Now, q(2a)=p, the magnitude of the electric dipole moment of the dipole. Therefore,
E=14π∈0.2pr(r2−a2)2 (along PX)
It may be noted that direction of electric field at a point on axial line of the dipole is from charge −q to +q, same as that of electric dipole moment of the dipole. If dipole is of very short length or when the point P is very far away from the electric dipole, then r2>>a2 and hence a2 can be neglected
E=14π∈0.2πrr4
E=14π∈0.2πrr3
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - NUMERICAL PROBLEMS10videos
ELECTRIC FIELD
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - NUMERICAL PROBLEMS (MOST EXPECTED QUESTIONS)4videos
ELECTRIC FIELD
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - SHORT ANSWER TYPE QUESTIONS7videos
ELECTRIC FIELD
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRIC CURRENT, RESISTANCE AND E.M.F.EXERCISE - MOST EXPECTED QUESTIONS14videos
ELECTRIC CURRENT, RESISTANCE AND E.M.F.
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRICAL DEVICESEXERCISE - (MOST EXPECTED QUESTIONS 2 MARK)2videos
ELECTRICAL DEVICES
Similar Questions
An electric dipoel consists of two equal and opposite charges placed 2 cm apart. When the dipole is placed in a uniform electric field of strength 105NC−1, it experiences a maximum torque of 0.2×10−3Nm. Find the magnitude of each charge.
07:05View SolutionA charged plastic spherical ball of mass 8.4×10−14kg is found to remain suspended in a uniform electric field of Entensity 5×102NC−1. Calculate the charge on the ball.
08:59View SolutionAre the electric field lines a reality ?
07:01View SolutionDefine SI unit of resistance.
06:31View SolutionWhy the core of a transformer made of a magnetic material of high permeability?
07:11View SolutionDerive an expression for the intensity of the electric field at a point on the axial line of an electric dipole.
05:34View SolutionDerive an expression for the intensity of the electric field at a point on the equatorial plane of an electric dipole.
03:21View SolutionDefine electric field intensity at a point. Give its S.I. units. Derive an expression for the electric field intensity at any point on the axial line of an electric dipole.
04:45View SolutionDerive an expression for electric potential due to a point charge
05:41View SolutionDerive the expression for electric intensity at a point on the axis of a dipole
03:13View SolutionDerive an expression for electric field intensity at a point on the axial line of an electric dipole.
05:15View SolutionWhat is an electric dipole? Derive an expression for the electric field intensity at a point on the axis of the dipole.
05:41View SolutionDerive an expression for the electric field intensity due to an electric dipole at any point on its equatorial line and show that the direction of the field is parallel to the axis of the dipole.
View SolutionDefine magnetic field intensity at a point and derive an expression for it at a point on the axial line of magnetic dipole. Also deduce the expression for small dipole.
View SolutionDefine electric field intensity. Derive an expression for electric field intensity on the axial line of an electric dipole.
05:06View SolutionWhat is magnetic dipole? Derive an expression for magnetic field intensity at a point on the equitorial line of a bar magnet.
View Solution

