Define phase of S.H.M. Show variation of displacement, velocity and acceleration with phase for a particle perfoming linear S.H.M. graphically, when it starts from extreme position.
A body starts rotating from rest. Due to a couple of $20 N m$ it completes $60$ revolutions in one minute. Find the moment of inertia of the body.

Video Solution

Text Solution

Verified by Experts

Phase of S.H.M. : The physical quantity which describes the state of oscillation of the particle perfoming S.H.M. i.e., it gives the displacement of the particle and its direction of motion from its equilibrium position.
In the equation of S.H.M.,
$x = A sin (ω t + ϕ)$
where, $(ω t + ϕ)$ is the phase angle of S.H.M.
Graphical representation of S.H.M. starting from extreme position:

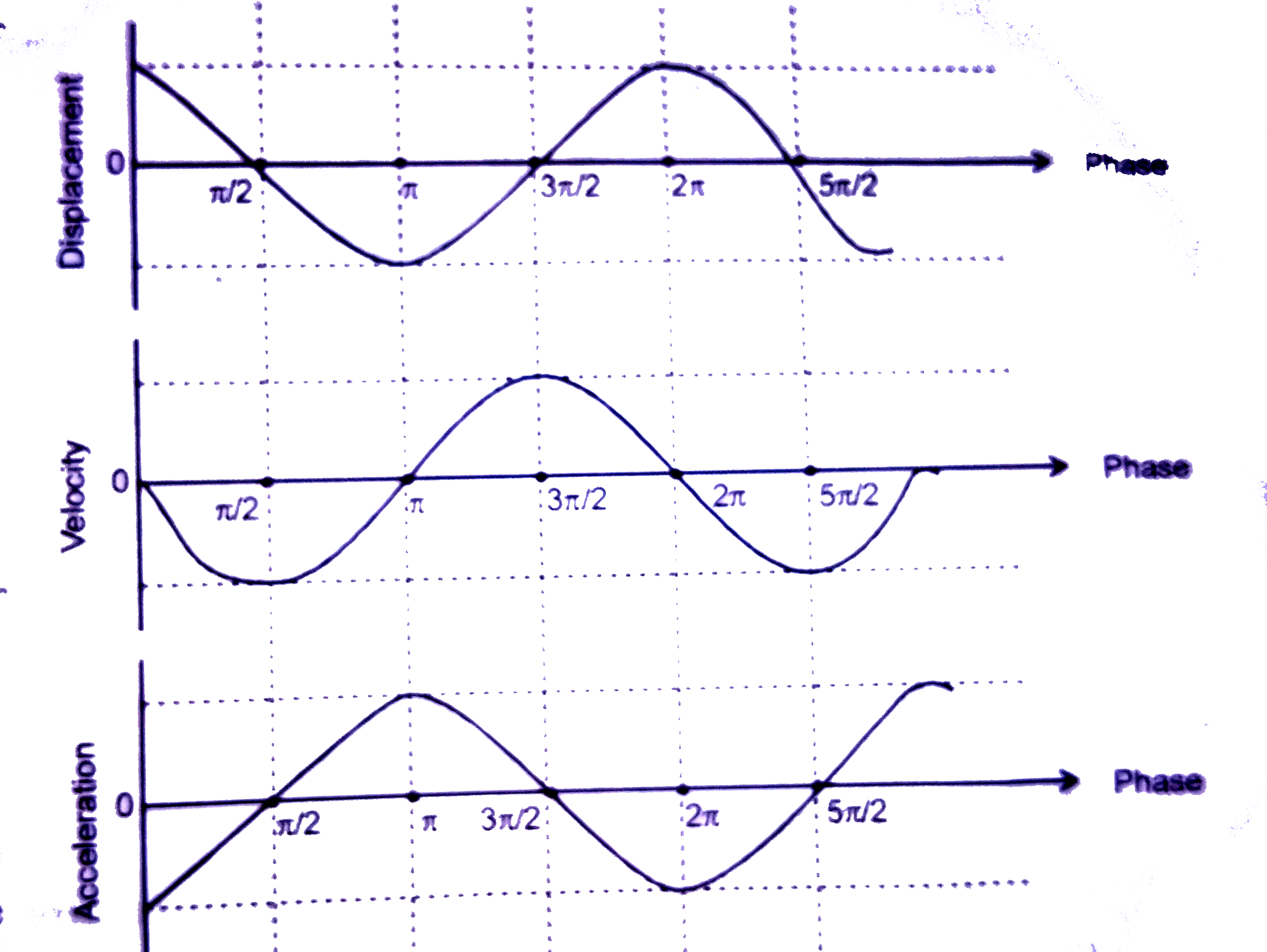
Numerical :
Given : Couple $(τ) = 20 N m$ ,
$n = 60$ rev in $1 a t m 1 min = 1 r . p . s$
$t = 1 min = 60 sec$
Now, $θ = ω t = 2 π n t$
$∴ θ = 2 π \times 1 \times 60 = 120 π$
Now, $θ = ω_{0} t + \frac{1}{2} α t^{2}$
$120 π = 0 + \frac{1}{2} α (60^{2})$ [ $∵ ω_{0} = 0$ ]
$α = \frac{240 π}{60 \times 60}$
$= \frac{π}{15} r a d / s^{2}$
As we know, $I = \frac{τ}{α}$
$I = \frac{20}{\frac{π}{15}}$
$= \frac{15 \times 20}{π}$
$= 95.48 k g m^{2}$

A particle performing S.H.M., its velocity when the particle moves from mean to extreme position is
Aslower initially and faster laterally
Buniformly moves
Cfaster initially and momentraily falls to zero
Dfast moves and stop at extreme position
A body starts rotating from rest and completes 10 revolutions in 4 s .Find its angular acceleration
A $2.5 π r a d / s^{2}$
B $5 π r a d / s^{2}$
C $7.5 π r a d / s^{2}$
D $10 π r a d / s^{2}$
A body starts ratating from rest and completes 100 revolutions in 20 s. Find its angular acceleration
A $π r a d s^{- 2}$
B $5 π r a d s^{- 2}$
C $4.5 π r a d s^{- 2}$
D $3.5 π r a d s^{- 2}$