Demonstrate that the potential of the field generated by a dipole with the electric moment p (fig) may be represented as φ=pr/4πε0r3, where r is the redius vector. Using this expression, find the magnitude of the electric strength vector as a funcition of r and θ.

Let two charges +q and −q be separated by a distance l. Then electric potential at a point at a distance r>>l from this dipole,
φ(r)=+q4πε0r++−q4πε0r−=q4πε0(r−−r+r+r−) (1)
But r−−r+=lcosθ and r+r−≅r2
From Eqs. (1) and (2).
φ(r)=qlcosθ4πε0r2=pcosθ4πε0r2φ=→p.→r4πε0r3
where p is magnitude of electric moment vector
Now, Er=−∂φ∂r=2pcosθ4πε0r3
and Eθ=−∂φr∂θ=pcosθ4πε0r3
So E=√E2r+E20=p4πε0r3√4cos2θ+sin2+θ

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Two point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

View SolutionA space is filled up with a charge with volume desnsity ρ=ρ0e−αr3, where ρ0 and α are positive constansts, r is the distance from the centre of this system. Find the magnitude of the electric field strength vector as a function of r. Investigate the obtained expresssion for the small and large values of r,i.e., at αr3<<1 and αr3>>1.
View Solution
Knowledge Check
A dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive direction of p and E, then the potential energy of the electric dipole is largest when θ is
Aπ4Bπ2CπDzeroA dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive directon of p and E, then the potential energy of electric dipole is larger when θ is-
Aπ4Bπ2CπDzeroThree identical dipoles are arranged as shown below. What will be the net electric field at P? (k=14πε0)
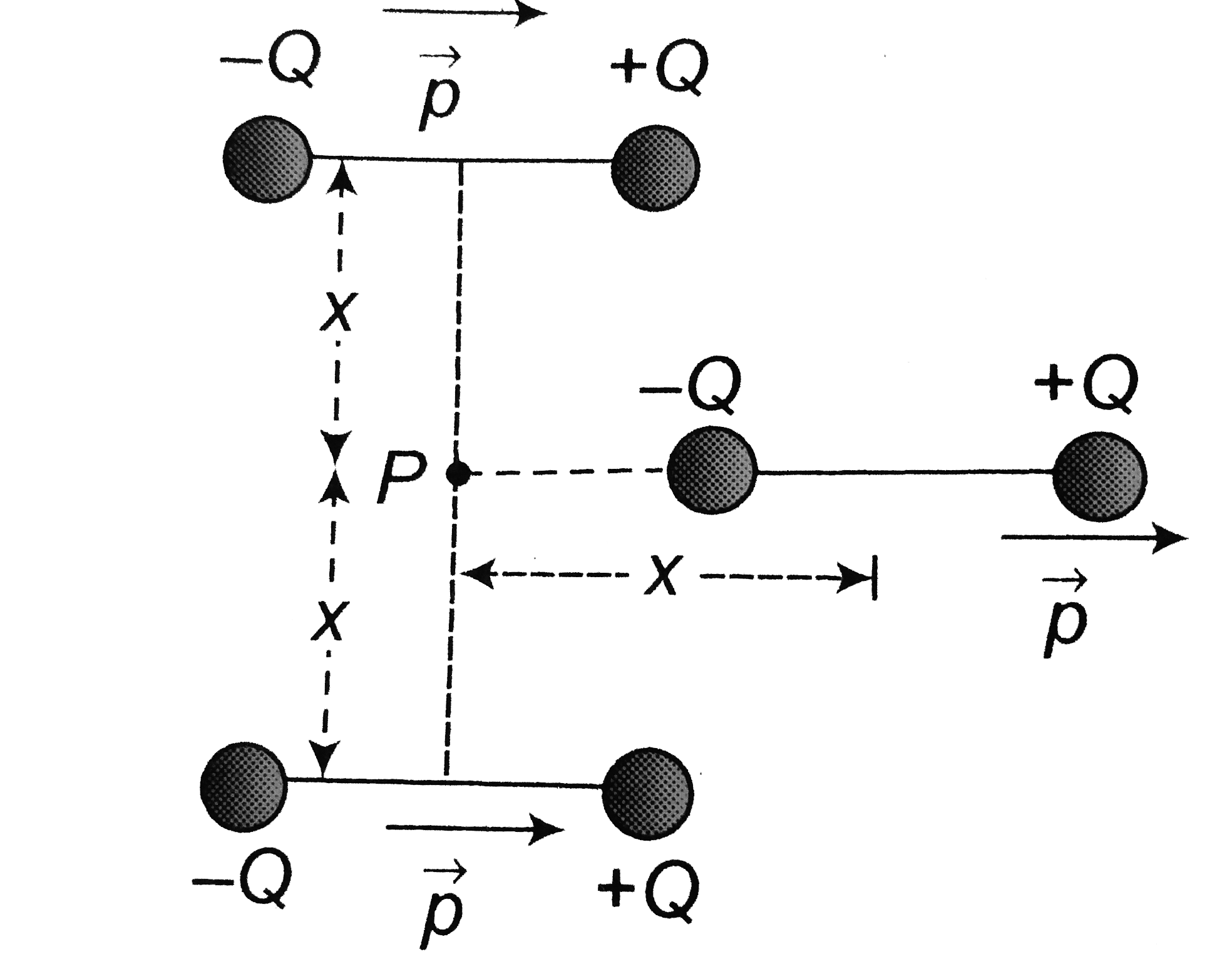 Ak.px3B2kpx3CZeroD√2kpx3
Ak.px3B2kpx3CZeroD√2kpx3
Two point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

View SolutionFind the electric field strength vector if the potentail of this field has the form φ=ar, where is a constatn vector, and r is the radius vector of point of the field.
View SolutionA dielectric ball is polarized uniformly and statically. Its polarization equals P. Taking into account that a ball ploarized is this way may be represented as a result of a small shift of all positive chagres of the dielectric relative to all negative charges,
(a) find the electric field strength E inside the ball,
(b) demonstrate that the field outside the ball is that of a dipole located at the centre of the ball, the potential of that field being equal to φ=p0r/4πε0, where p0 is the electric moment of the ball, and r is the distance from its centre.
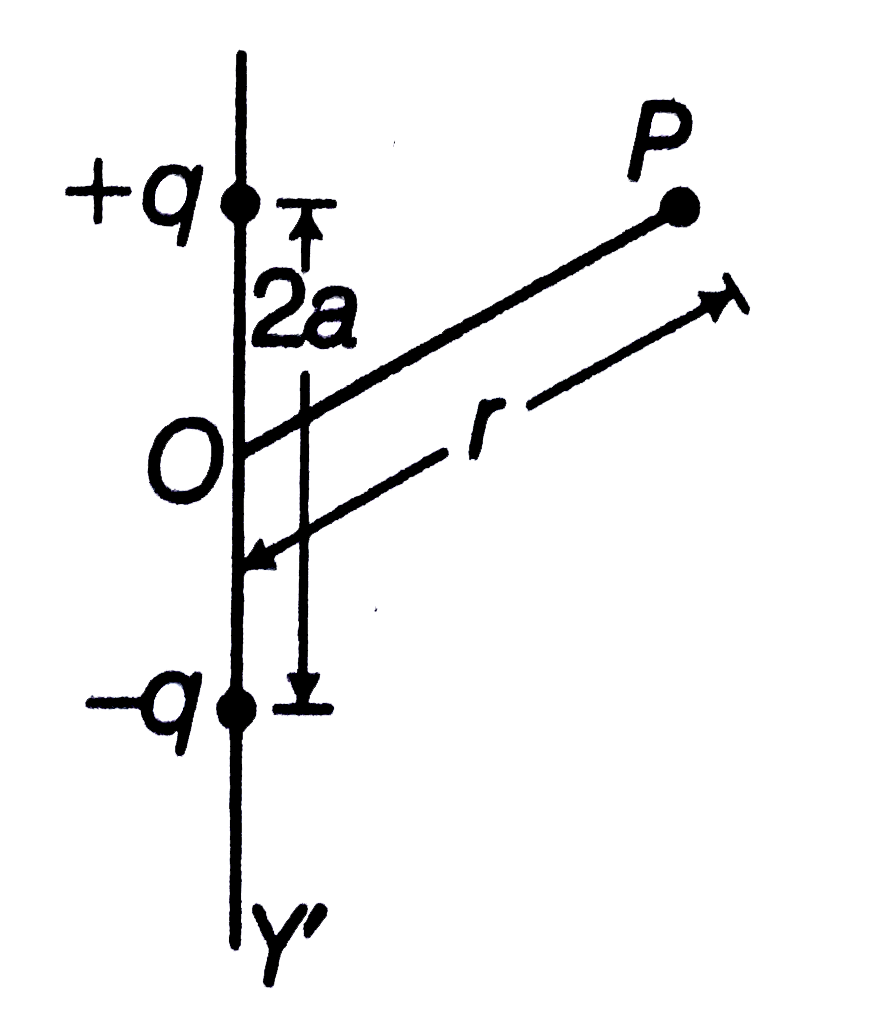
View SolutionWhat is the electric potential at a point P, distance r from the mid-point of ann electric dipole of moment p(=2aq) ?
View SolutionThe variation of potential V with distance r from dixed point is shown in Fig. The magnitude of electric field at, r=2cm (in volt/cm) is :
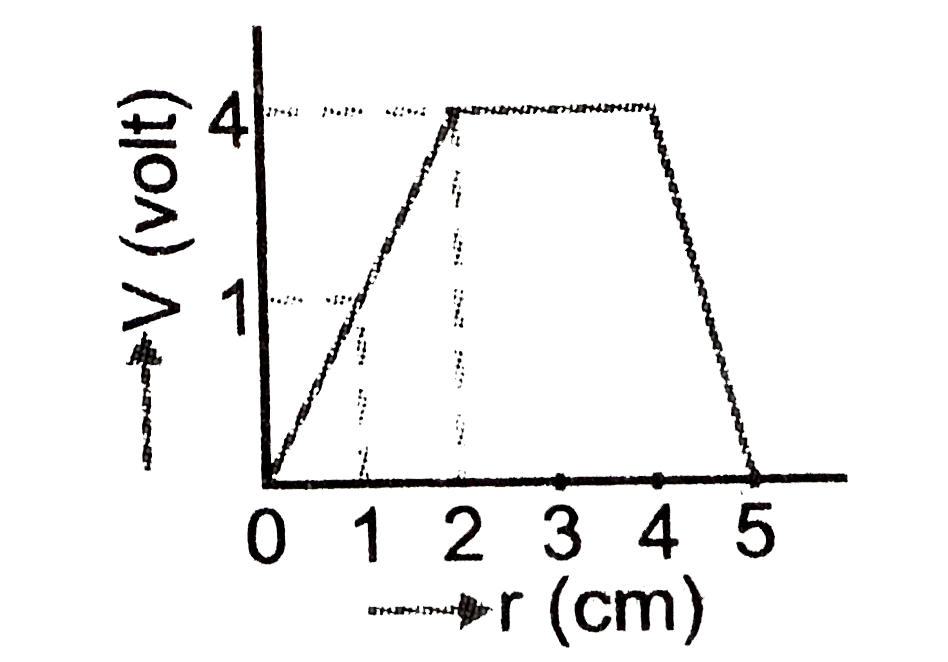
View Solution
