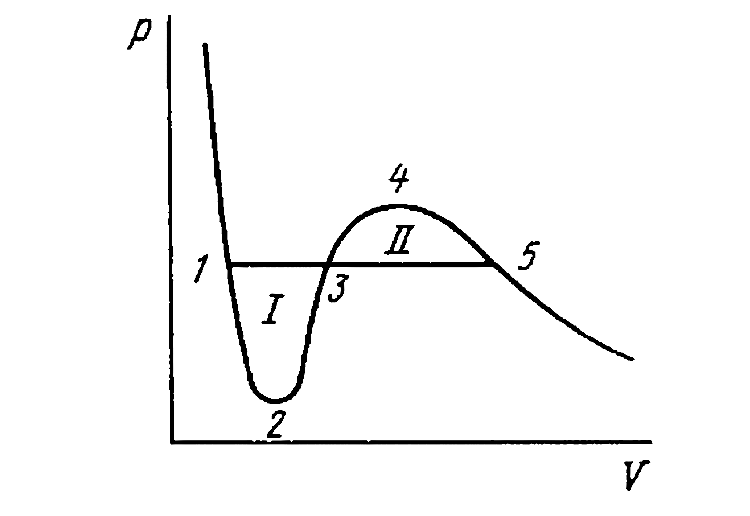
Demonstrate that the straight line 1−5 corresponding to the isothermal-isobaric phase isotherm so that areas I and II are equal (Fig. 2.5).
 .
.
We apply the relation (T=constant)
T∮dS=∮dU+∮pdV
to the cycle 1234531
Here ∮dS=∮dU=0
So ∮pdV=0
This implies that the areas I and II are equal. This reasoning is inapplicable to the cycle 1231, for example. This cycle is irreverisble because it involves the irreverible transition from a single phase to a two-phase state at the point 3.
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
The wave number of a spectral line is 5×105m−1. The energy corresponding to this line is
A3.49×10−23 kJB4.45×10−24 JC5.50×10−22 JD9.93×10−23 kJIf the straight lines x+2y=9,3x−5y=5 and ax+by=1 are concurrent , then the straight line 5x+2y=1 passes through the point
A(a,−b)B(−a,b)C(a,b)D(−a,−b)
A volume occupied by a saturated vapour is reduced isothermally n−fold. Find what fraction η of the final volume is occupied by the liquid phase if the specific volumes of the saturated vapour and the liquid phase differ by N times (N>n). Solve the same problem under the condition that the final volume of the substance corresponds to the midpoint of a horizontal portion of the isothermal line in the diagram p,V.
View SolutionFind the equation to the straight line which passes through the point (5,6) and has intercepts on the axes. i)equal in magnitude and both postive ii)equal in magnitude but opposite in sign
View SolutionExplain whether (a) T2>T1, (b) P2>P1 and (c ) V2>V1 or otherwise in Fig., which represent in isothermal, isobaric, and isochoric processes for the same mass of an ideal gas, respedtively.

View SolutionIf the straight line 3x+4y=8 denoted by 'L' then the points (2−5) and (−5,2)
View SolutionDemonstrate that Eqs. (2.6a) and (2.6b) are valid for a substance, obeying the Van der Qaals equation, in critical state
Make use of the fact that the critical state corresponds to the point of inflection in the isothermal curve p(V).
View SolutionThe amount of heat supplied to an ideal gas is laid off on the horizontal axis and the amount of work performed by the g-as is laid off on the vertical axis. One of the straight lines in the ligure is an isotherm and the other two are isobars of two gases. The initial states of hoth gases (pressure, temperature, volume) are the same, and the scales on the two axes coincide. Which straight line corresponds to which process? How many degrees of freedom does each gas have? (Vibrational degrees of freedom are not to be taken into account.) The graphs of what processes coincide with the coordinate axes?
View Solution