Derive an expression for a thin double convex lens. Can you apply the same to a double concave lens too?

Text Solution

Verified by Experts

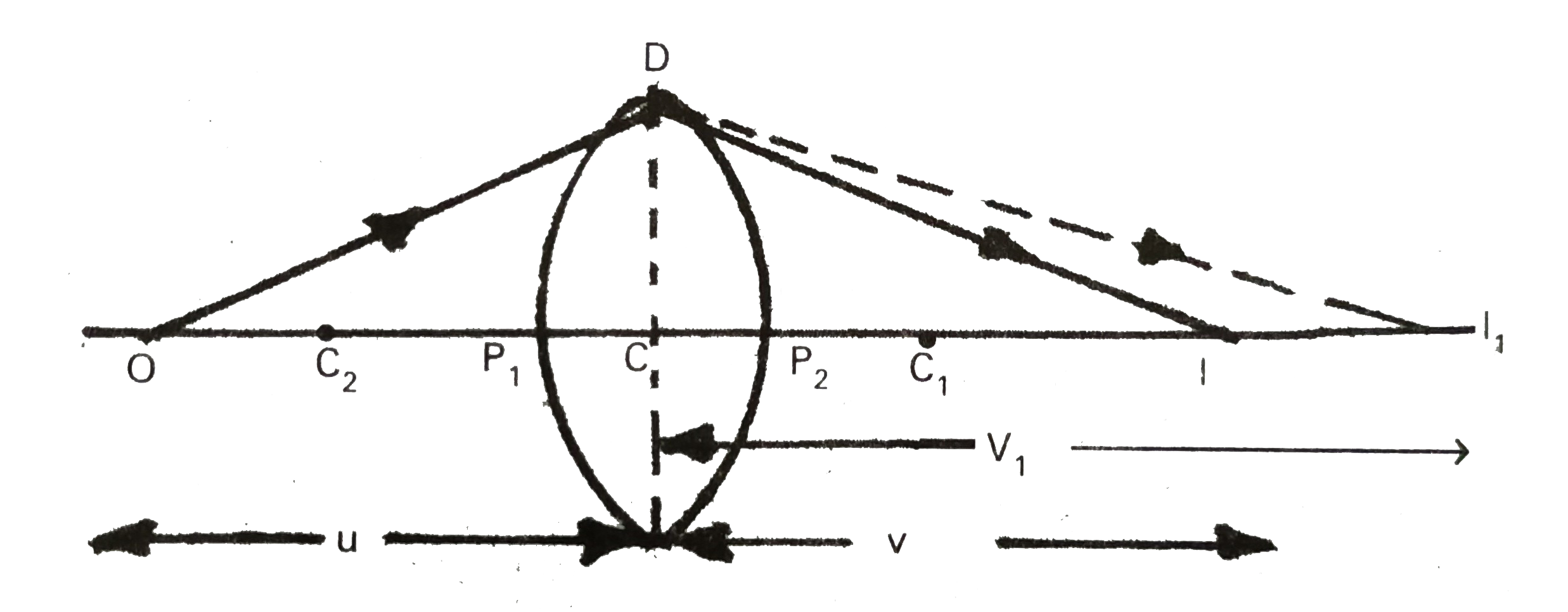
i) convex lens is made up of two spherical refracting surfaces of radii of curvatures, $R_{1} and R_{2} and μ$ is the refractive index of the lens.
ii) $P_{1}, P_{2}$ and the poles, $C_{1}, C_{2}$ are the centres of curvatures of two surfaces with optical centre C.
iii) Consider a point object O lying on the principal axis of the lens and $I_{1}$ is the real image of the object.
If $C I_{1} \approx P_{1} I_{1} = v_{1}$
and ${CC}_{1} \approx P C_{1} = R_{1}$
$C O \approx P_{1} O = u$
iv) As refraction is taking place from rarer to denser medium
$\frac{μ_{1}}{- u} + \frac{μ_{2}}{v_{1}} = \frac{μ_{2} - μ_{1}}{R_{1}} ..................................(1)$
v) The refracted ray suffers further refraction
Therefore I is the final real image of O.
vi) For refraction at second surface, $I_{1}$ as virtual object, whose real image is formed at I,
$∴ u \approx C I_{1} \approx P_{2} I_{1} = V_{1}$
$Let C I \approx P_{2} I = V$
vii) Now refraction taking place from denser to rarer medium
$\frac{- μ_{2}}{v_{1}} + \frac{μ_{1}}{v} = \frac{μ_{1} - μ_{2}}{R_{2}} = \frac{μ_{2} - μ_{1}}{- R_{2}} ...................(2)$
Adding equations (1) and (2)
$\frac{μ_{1}}{- u} + \frac{μ_{1}}{v} = (μ_{2} - μ_{1}) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$μ_{1} = (\frac{1}{v} - \frac{1}{u}) = (μ_{2} - μ_{1}) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$\frac{1}{v} - \frac{1}{u} = (\frac{μ_{2}}{μ_{1}} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}}) (∵ μ = \frac{μ_{2}}{μ_{1}})$
$\frac{1}{v} - \frac{1}{u} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}}) ....................(3)$
When the object on the left of the lens is at infinity $(\propto)$ , image is formed at principal focus of the lens.
$∴ u = \propto, υ = f = focal length of the lens.$
$\frac{1}{f} - \frac{1}{\propto} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$\frac{1}{f} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}}) ........................(4)$
This is the lens marker's formula.
Yes, same formula applies to double concave lens too.

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $R_{1}$ and $R_{2}$ are the radii of curvature of double convex lens made of same material, the lens with more focal length is
A $R_{1} = 20 c m, R_{2} = 10 c m$
B $R_{1} = R_{2} = 20 c m$
C $R_{1} = R_{2} = 10 c m$
D $R_{1} = R_{2} = 5 c m$

VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-RAY OPTICAL AND INSTRUMENTS-LONG ANSWER QUESTIONS

Home
Ask Doubt
Profile