Derive an expression for electric flux of rectangular area placed in uniform electric field. Solution in Tamil
(i) Electric flux for uniform electric field: Consider a uniform electric field in a region of space. Let uschoose an area A normal to the electric field lines as shown in figure (a).
The electric flux for this case is
ΦE=EA ...(1)
Suppose the same area A is kept parallel to the uniform electric field, then no electric field lines pierce through the area A, as shown in figure (b). The electric flux for this case is zero.
ΦE=0 ....(2)
If the area is inclined at an angle θ with the field, then the component of the electric field perpendicular to the area alone contributes to the electric flux. The electric field component parallel to the surface area will not contribute to the electric flux. This is shown in figure (c ). For this case, the electric flux
ΦE=(Ecosθ)A ....(3)
Further, θ is also the angle between the electric field and the direction normal to the area. hence in general, for uniform electric field. The electric flux is defined as
ΦE=→E.→A = EA cosθ ....(4)

Here, note that →A is the area vector →A=Aˆn. Its magnitude is simply the area A and the direction is along the unit vector ˆn perpendicular to the area. Using this definition for flux. ΦE=→E.→A.equations (2) and (3) can be obtained as special cases.
In figure(a), θ=0∘ so ΦE=→E.→A=EA
In figure (b), θ=90∘soΦ1=→E.→A=0
(ii) Electric flux in a non uniform electric field and an arbitrarily shaped area: Suppose the electric field is not uniform and the area A is not flat, then the entire area is divided into n small area segments Δ−→A1,Δ−→A2,Δ−→A3,........Δ−→An, such that each area element is almost flat and the electric field over each area element is considered to be uniform .
The electric flux for the entire area A is approximately written as
ΦE=−→E1.Δ−→A1+−→E2.Δ−→A2+−→E3.Δ−→A3+.......+−→En.Δ−→An=n∑i=l−→Ei.Δ−→Ai .... (5)
By taking the limit Δ−→A1→θ (for all i) the summation in equation (5) becomes integration . the total electric flux for the entire area is given by
ΦE=∫→E.d→A ....(6)
From Equation (6), It is clear that the electric flux for a given surface depends on both the electric field pattern on the surface area and orientation of the surface with respect to the electric field.
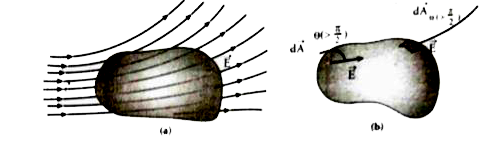
(iii) Electric flux for closed surfaces : In the previous section, the electric flux for any arbitrary curved surface is discussed Suppose a closed surface is present in the region of the non-uniform electric field as shown in figure (a).
The total electric flux over this closed surface is written as
ΦE−∮E.d→A ....(7)
 Note the difference between equations (6) and (7) the integration equation (7) is a closed surface integration and for each areal element, the outward normal is the direction of d→A as shown in the figure (b).
Note the difference between equations (6) and (7) the integration equation (7) is a closed surface integration and for each areal element, the outward normal is the direction of d→A as shown in the figure (b).
The total electric flux over a closed surface can be negative,
Positive or zero. In the figure (b), it is shown that in one area element , the angle between d→Aand→E is less than 90∘, then the electric flux is positive and in another areal element, the angle between d →Aand→E is greater than 90∘ , then the electric flux is negative.
In general, the electric flux is negative if the electric field lines enter the closed surface and positive if the electric field lines leave the closed surface.
Topper's Solved these Questions
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - ADDITIONAL QUESTIONS SOLVED ( VII. NUMERICAL PROBLEMS )
5 Videos
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - ADDITIONAL QUESTIONS SOLVED ( V. SHORT ANSWER QUESTIONS: )
8 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - FULL MARKSCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )
10 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
4 Videos
Similar Questions
Electrons are caused to fall through a potential difference of 1500 volts. If they were initially at rest. Then calculate their final speed.
View SolutionWhat is meant by triboelectric charging ?
View SolutionIf a light of wavelength 4950 Å is viewed as a continuous flow of photons, what is the energy of each photon in eV ? (Given h=6.6×10−34Js, c =3×108ms−1)
View SolutionThe radius of the first orbit of hydrogen atom is 0.5 Å. The electron moves is an orbit with a uniform speed of 2.2×106ms−1. What is the magnetic field produced at the centre of the uncleus due to the mation of this electron ? Use μ0=4π×10−7Hm−1 and electric charge =1.6×10−19 C
View SolutionDerive an expression for the potential energy of an electric dipole placed in a uniform electric field.
View Solutionसमरूप विद्युत क्षेत्र में विद्युत द्विध्रुव को घुमाने में किये गये कार्य का व्यंजक व्युतपन्न कीजिए |
View SolutionDerive an expression for potential energy of electric - di-pole placed in a n uniform electric field .
View SolutionDerive an expression for potential energy of electric-dipole placed in an uniform electric field.
View SolutionDerive an expression for the torque acting on an electric dipole placed in a uniform electric field.
View SolutionDerive an expression for torque experiencedby electric dipole in a uniform electric field
View SolutionDerive the expression for torque on an electric dipole placed in a uniform electric field.
View SolutionDerive the expression for the couple acting on the electric dipole in uniform electric field
View SolutionDerive an expression for torque acting on an electric dipole in uniform electric field.
View SolutionDerive an expression for couple acting on an electric dipole kept in a uniform electric field.
View SolutionArea Vector|Electric Flux|Electric Flux Produced By Point Charge|Electric Flux In Non Uniform Electric Field
View Solution
