Derive an expression for the electric potential at a point along the axial line of an electric dipole.Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

Magnetic dipole: A pair of magnetic poles having equal and opposite pole strength separated by a small distance is known as magnetic dipole. Magnetic field intensity: Magnetic field intensity at a point is defined as the force experienced by a unit north pole when placed at that point.
Magnetic field at a point on the axial line of the magnetic dipole: Let we have a bar magnet NS having length 2l.
O is the mid-point of the magnetic dipole. Let m= Pole strength of each pole of the magnet (magnetic dipole) Let P is any point on the axial line of magnet at a distance r from the centre of magnetic dipole.

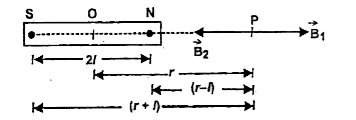
Let $O P = r, ∴ N P = (r - l) and S P = (r + l)$
Let a unit north pole is placed at P. then magnetic field at P due to N-pole of magnet
${\to B}_{1} = \frac{μ_{0}}{4 π} \frac{m}{{(N P)}^{2}} = \frac{μ_{0}}{4 π} \frac{m}{{(r - l)}^{2}}$ along $- - \to N P$
or ${\to B}_{1} = \frac{μ_{0}}{4 π} \frac{m}{{(r - l)}^{2}}$ along $- - \to N P$ (produced)
Magnetic field at P due to S-pole of the magnet
${\to B}_{2} = \frac{μ_{0}}{4 π} \frac{m}{{(S P)}^{2}}$ along $- \to P S$
or ${\to B}_{2} = \frac{μ_{0}}{4 π} \frac{m}{{(r + l)}^{2}}$ along $- \to P S$
As $∣ ∣ {\to B}_{1} ∣ ∣ > ∣ ∣ {\to B}_{2} ∣ ∣$
$∴$ Magnetic field at P due to bar magnet
$B = B_{1} - B_{2}$ [In magnitude]
$= \frac{μ_{0}}{4 π} [\frac{m}{{(r - l)}^{2}} - \frac{m}{{(r + l)}^{2}}]$
$= \frac{μ_{0} m}{4 π} [\frac{{(r + l)}^{2} - {(r - l)}^{2}}{{(r^{2} - l^{2})}^{2}}]$
$B = \frac{μ_{0} m}{4 π} \frac{4 r l}{{(r^{2} - l^{2})}^{2}} = \frac{μ_{0}}{4 π} \frac{2 r (m .2 l)}{4 π {(r^{2} - l^{2})}^{2}} [∵ m (2 l) = M]$
$∴ B = \frac{μ_{0}}{4 π} \frac{2 M r}{{(r^{2} - l^{2})}^{2}}$ along NP produced
For a short magnet or a small magnetic dipole: i.e., when $l^{2} < < r^{2}$
Then, $\to B = \frac{μ_{0}}{4 π} \frac{2 \to M}{{(r^{2})}^{2}}$
$\to B = \frac{μ_{0}}{4 π} \frac{2 - - \to M r}{{(r^{2})}^{2}}$
$\to B = \frac{μ_{0}}{4 π} \frac{2 \to M}{r^{3}}$

|

Updated on:21/07/2023

Class 12 PHYSICS MAGNETIC DIPOLES AND EARTH'S MAGNETISM

Topper's Solved these Questions

Similar Questions

BETTER CHOICE PUBLICATION-MAGNETIC DIPOLES AND EARTH'S MAGNETISM-Long answer type questions

Home
Ask Doubt
Profile