Derive an expression for the torque acting on a current carrying loop suspended in a uniform magnetic field.Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

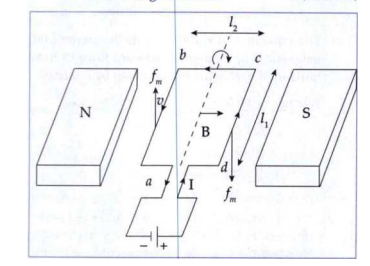
1. As shown in figure, consider a rectangular coil ABCD suspended in a uniform magnetic field $\vec{B}$ , with its axis perpendicular to the field.

2. Suppose, current flowing through coil ABCD be I, AB = DC = b and AD = BC = a and area be A = ab.
2. The field exerts no force on the two arms AD and BC of the loop, because $I_{a} and \vec{B}$ both are parallel to each other,
$| \vec{F} | = | I \vec{a} \times \vec{B} |$
$| \vec{F} | = (I a \times B) {\sin 0}^{\circ} = 0 ... (1)$
3. Sides AB and CD of coils are perpendicular to magnetic field.
4. So, force on side AB is,
${\vec{F}}_{1} = | I \vec{b} \times \vec{B} | = I b sin \frac{π}{2}$
$| {\vec{F}}_{1} | = I b B ... (2)$
5. Similarly it exerts a force ${\vec{F}}_{2}$ on the arm CD and ${\vec{F}}_{2}$ is directed out of the plane of the paper,
$| {\vec{F}}_{2} | = | I \vec{b} \times \vec{B} | = | I b sin \frac{π}{2} |$
$∴ F_{2} = I b B = F_{1} ... (2)$
6. Thus, the net force on the loop is zero. There is a torque on the loop due to the pair of forces ${\vec{F}}_{1} and {\vec{F}}_{2}$ .
7. Figure (b) shows a view of the loop from the AD end. It shows that the torque on the loop tends to rotate it anti-clockwise.
8. Resultant torque on coil is given by,
$τ = τ_{1} + τ_{2}$
$τ = F_{1} (\frac{a}{2}) + F_{2} (\frac{a}{2})$
= $I b B (\frac{a}{2}) + I b B (\frac{a}{2})$
= $I (a b) B$
$τ = I A B ... (3)$
where A = ab that is area of rectangle.

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-MOVING CHARGES AND MAGNETISM-SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)

Home
Ask Doubt
Profile