Question

Derive an expressions for the kinetic energy and velocity on an inclined plane of inclination $\theta$ for the body rolling without sliding.

Explanation

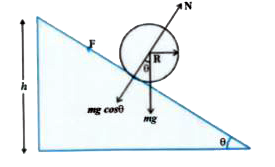
Consider a body of mass m, moment of inertia about its geometric axis I, radius of gyration k, geometric radius R rolling down an inclined plane of inclination `theta` and height h without slipping.
Here body is rolling without slipping so it centre of mass moves with linear velocity and body rotates about its axis concide with axis of rotation. Hence motion of body is the combine motion of translation and rotation. These both motoins can be describe separately.
If the total kinetic energy of body is k, then
k = translational kinetic energy + rotational kinetic energy
`k=(1)/(2)mv_(cm)^(2)+(1)/(2)Iomega^(2)`
but `I=mk^(2)` where k = radius of gyration and `v_(cm)=Romega`
`therefore k=(1)/(2)mv_(cm)^(2)+(1)/(2)mk^(2)xx(v_(cm)^(2))/(R^(2))[because omega=(v_(cm))/(R)]`
`therefore k=(1)/(2)mv_(cm)^(2)[1+(k^(2))/(R^(2))]`
is a formula for kinetic energy of rolling body it can applies to disc, ring or sphere also.
Now compare k with potential energy mgh
`mgh=(1)/(2)mv^(2)[1+(k^(2))/(R^(2))][because v_(cm)=v]`
`therefore v^(2)=(2gh)/([1+(k^(2))/(R^(2))]).`
Velocity at bottom for this rolling body
`v=[(2gh)/(1+(k^(2))/(R^(2)))]^((1)/(2))`