Describe the motion corresponding to x−t equation, x=10−4cosωt.
Simple harmonic with mean at x=10, amplitude 4 and extreme position at x=6 and x=14. At t=0, it starts from x=6. Here, x is coordinate, not displacement from mean position.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.3
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.4
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Knowledge Check
A particle moves along the x-axis according to the equation x=asinωt+bcosωt. The motion is simple harmonic with
Atime period 2π/ωBamplitude √a2+b2Camplitude a+bDamplitude a-bThe oscillation of a body on a smooth horizontal surface is represented by the equation, X=Acos(ωt)
where X = displacement at time t
ω = frequency of oscillation
Which one of the following graphs shows correctly the variation a with t ?A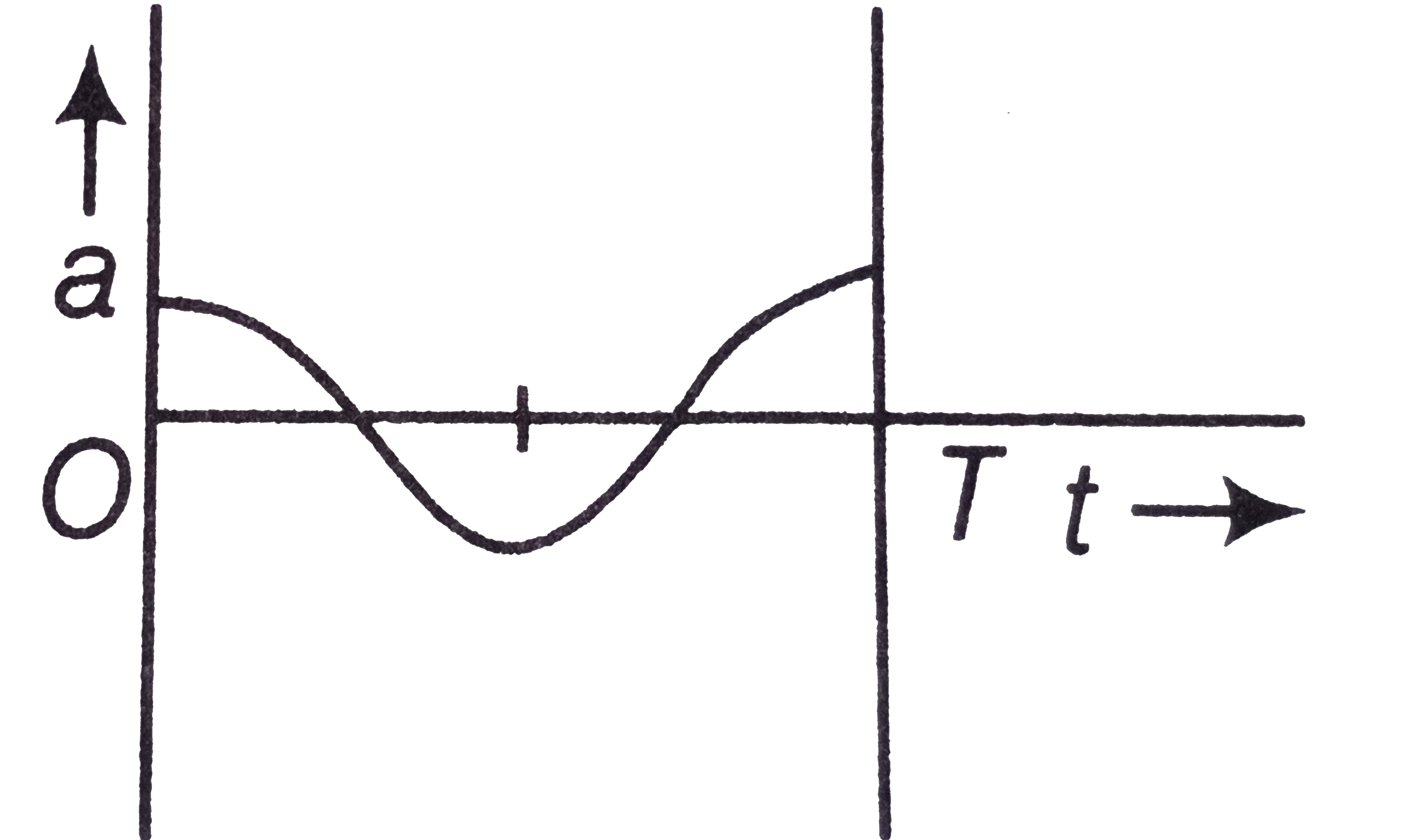 B
B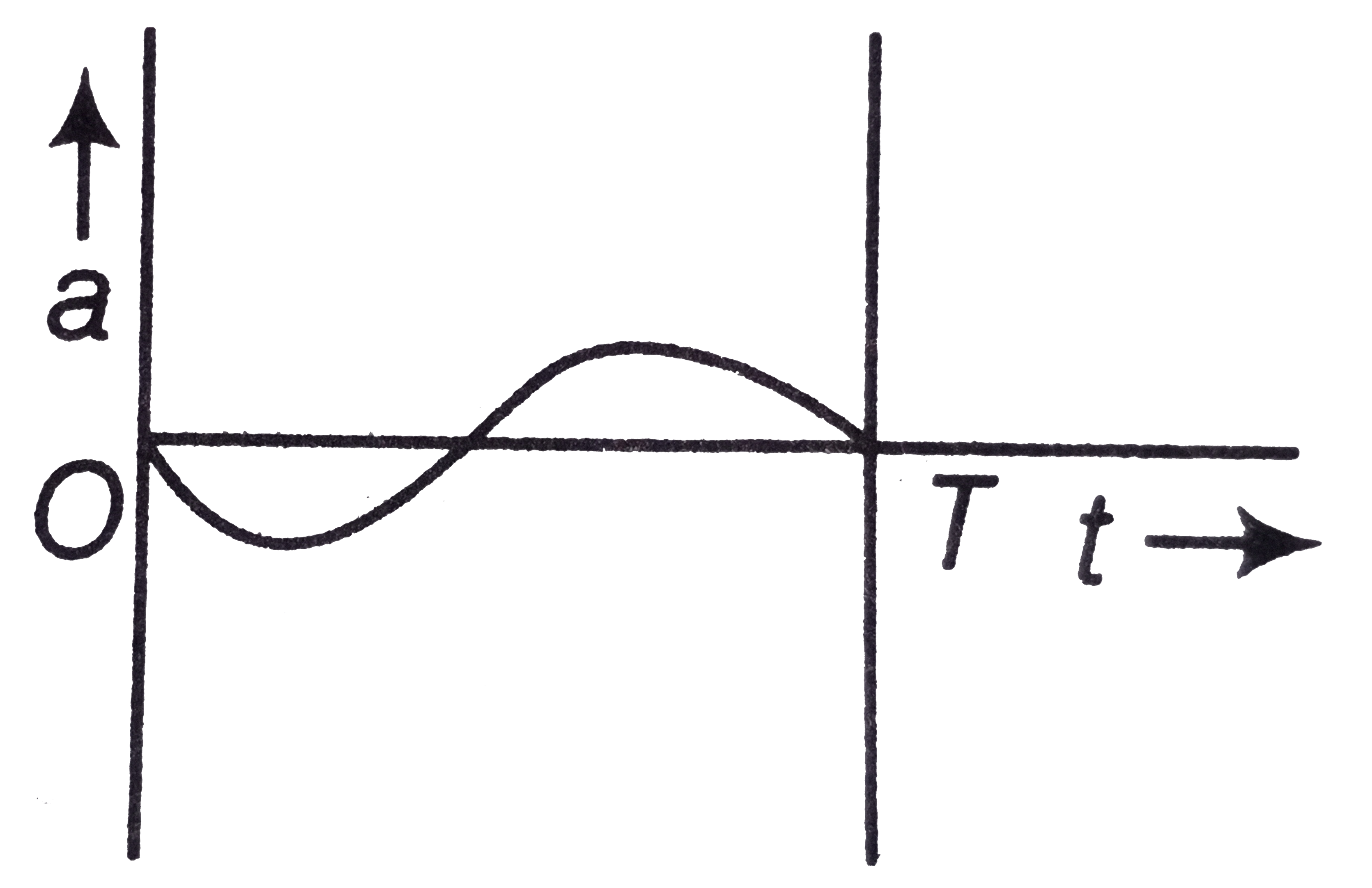 C
C D
D
A particle move along y-axis according to equation y+3+4cosωt. The motion of the particle is
AcircularBperiodic but not SHMCSHMDoscillatory but not SHM
The oscillation of a body on a smooth horizontal surface is represented by the equation,
X=Acos(ωt)
where, X = displacement at time t
ω= frequency of oscillation
Which one of the following graphs shows correctly the variation a with t?
Here, a = acceleration at time t
T = time period
View SolutionA particule moves in x - y plane acording to rule x = a sin ωt and y = a cos ωt. The particle follows
View SolutionThe SHM of a particle is given by the equation x=2sinωt+4cosωt. Its amplitude of oscillation is
View SolutionAssertion : In x=Acosωt, x is the displacement measured from extreme position.
Reason : In the above equation x=A at time t=0.
View SolutionA particle moves in x-y plane according to the equation ¯r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View Solution
