Determine the luminosity of a surface whose luminance depends on direction as , where is the angle between the radiation direction and the normal to the surface.
Luminance is the light energy emitted per unit area o fthe emitting surface in a given direction per unit solid angle divided by . Luminosity is simply enegry emitted per unit area.
Thus
where the integration must be in the forward hemisphere of the emitting surface (assuming light is being emitted in only one direction say outward direction of the surface) But
Thus
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A point source is suspended at a hight h=1.0m over the centre of a round table of radius R=1.0m. The luminous intensity I of the source depends on direction so that illuminance at all points of the table is the same. Find the function I(θ), where θ is the angle between the radiation direction and the vertical, as well as the luminous flux reaching the table if I(0)=I0=100cd.
View SolutionShow that the electric field at the surface of a charged conductor is given by →E=σε0ˆn , where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction .
View Solution
Knowledge Check
A parallel beam of monochromatic light is incident on the surface of water having refractive index 4/3. The direction of the incidence beam bisects the angle between the normal to the water surface and the water surface. The angles of incidence and refraction are
Ai=30∘,r=20∘Bi=45∘,r=20∘Ci=45∘,r=32∘Di=60∘,r=40∘Assertion : If θ is the angle between the planes of transmission of two analysers then the intensity of emergent light is proportional to cos∘θ.
Reason : In the propagation of electromagnetic waves, the angle between the direction of propogation and plane of polarisation is π2.AAssertion is True, Reason is True, Reason is a correct explanation for AssertionBAssertion is True, Reason is True, Reason is not a correct explanation for AssertionCAssertion is True, Reasonis FalseDAssertion is False, Reason is TrueIf l1,m1,n1 and l2,m2,n2 are the directional cosines of two vectors and θ is the angle between them, then their value of cosθ is
Al1l2+m1m2+n1n2Bl1m1+m1n1+n1l1Cl2m2+m2n2+n2l2Dm1l2+l2m2+n1m2
A point source is suspended at a height h over the centre of a round. Table The lumious intensity. P of the source depends on the direction θ with the normal function Pθ in terms of θ, assuming thatP(0)=P0
View SolutionProve that the equation of the normal to x23+y23=a23 is ycosθ−xsinθ=acos2θ, where θ is the angle which the normal makes with the axis of x.
View SolutionA semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
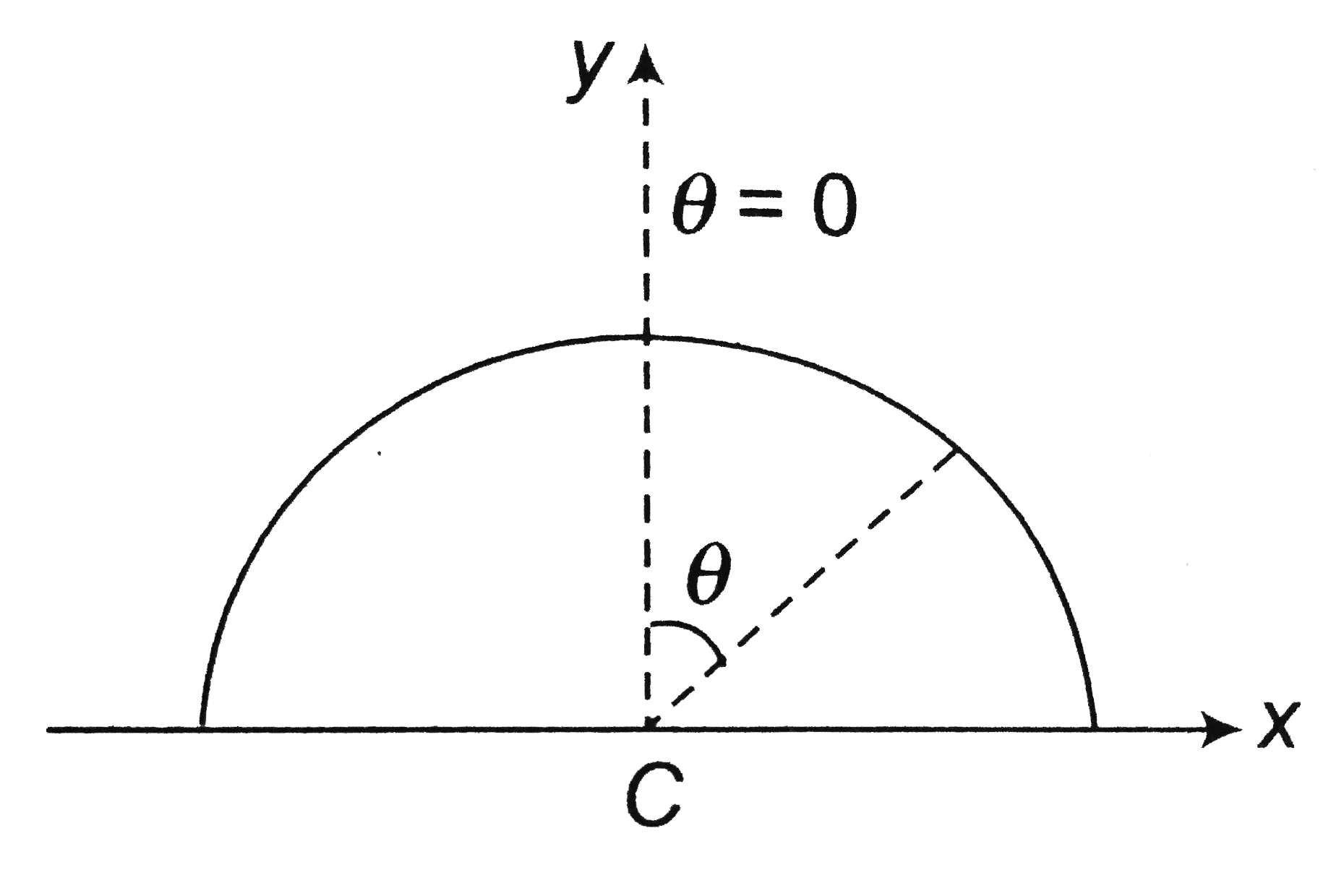
View SolutionA beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
View SolutionA time varying force is applied on a block placed over a rough surface as shown in figure. Let θ be the angle between net contact force on the block and the normal reaction, then with time, θ will
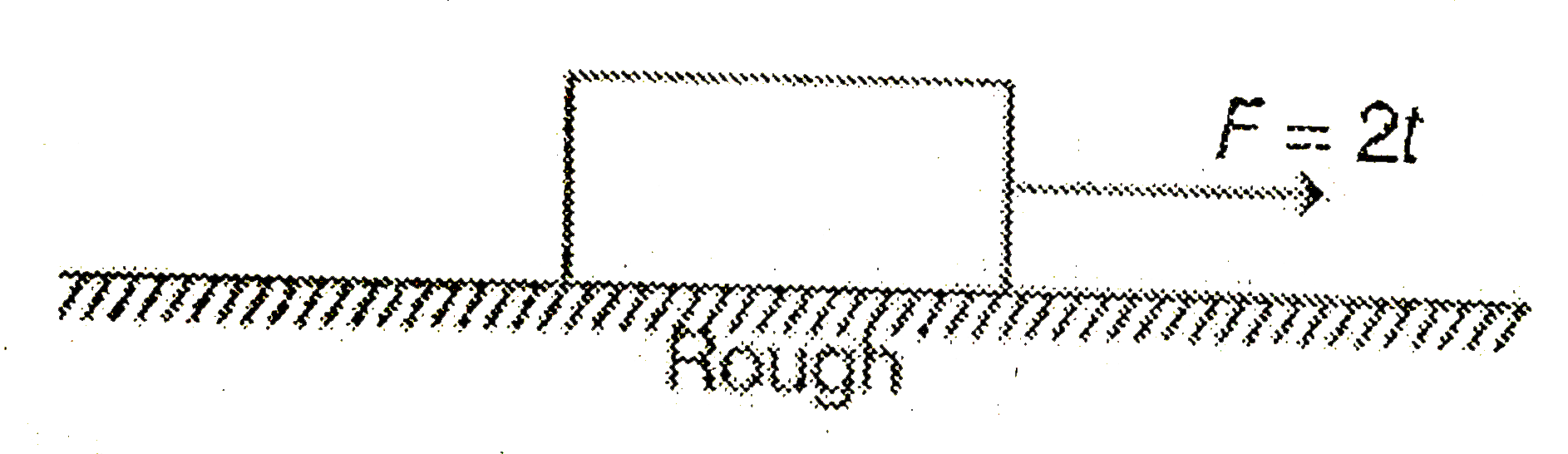
View Solution
