Develop the notions of work and kinetic energy and show that it leads to work-energy theorem.
Consider a drop of mass 1.00 g falling from a height of 1.00 km. What is the work done by the gravitational force ? (Take g = 10 ms−2)
Work : Work done by a force is defined as the product of component of force in the direction of displacement and the magnitude of displacement.
W=¯¯¯F.¯¯¯S
When ¯¯¯Fand¯¯¯S are parallel
W=∣∣¯¯¯F∣∣×∣∣¯¯¯S∣∣
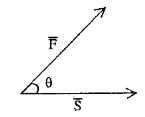
When ¯¯¯Fand¯¯¯S has some angle θ between them
W=¯¯¯F.¯¯¯Scosθ
Kinetic energy : Energy possessed by a moving body is called kinetic energy (K).
The kinetic energy of an object is a measure of the work that an object can do by the virtue of its motion.
Kinetic energy can be measured with equation K=12mv2
Ex : All moving bodies contain kinetic energy.
Work energy theorem (For variable force) : Work done by a variable force is always equal to the change in kinetic energy of the body.
Work done W=12mV2−12mV20=Kf−Ki
Proof : Kinetic energy of a body K=12mv2
Time rate of change of kinetic energy is
dkdt=ddt(12mv2)=12m.2v.dvdt=mv.dvdtButdvdt=a
∴dkdt = mav but ma = Force (F)
∴dkdt=Fv=F.dxdtordkdt=F.dxdtordk=F.dx
When force is conservative force F = F(x)
∴ On integration over initial position (x1) and final position x2
∫fidk=∫x2x1F(x)dx but∫x2x1F(x)dx = work done
By variable force W
∴W=∫fidk⇒W=Kf−Ki
i.e. work done by a conservative force is equal to change in kinetic energy of the body.
Problem :
Mass = 1g = 1×10−3 kg,
height h = 1 km = 103 m,
g = 10 m/s2
Work done by gravitational force W = mgh
∴W=1×10−3×103×10=10J
Topper's Solved these Questions
Similar Questions
Knowledge Check
A body of mass 10 kg is dropped to the ground from a height of 10 metres. The work done by the gravitational force is (g=9.8m/sec2)
A−490 joulesB+490 joulesC−980 joulesD+980 joulesA stone of mass 20 g falling from height of 2 km hits the ground with a speed of 200ms−1. The work done by the gravitational force is
A100JB200JC300JD400JA drop of mass 1.00g falling from a height 1.00km. It hits the ground with a speed of 50.0ms−1. What is the work by the unknown resistive force ?
A−8.75JB8.75JC−4.75JD4.75J
It is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of 50.0ms−1 (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionIt is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of 50.0ms−1 (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionA raindrop of mass 1.00 g is falling from a height of 1.00 km. It hits the ground with a speed of 50.0ms−1Find the work done
by the unknown resistive force (g=10ms2).
View SolutionA raindrop of mass 1g falling from a height of 1km hits is the ground with a speed of 50ms−1. Which of the following statements is correct? (Takingg=10ms−2).
View SolutionA raindrop of mass 1g falling from a height of 1km hits is the ground with a speed of 50ms−1. Which of the following statements is correct? (Takingg=10ms−2).
View Solution
