Dimensions of ε0dϕEdt are same as that of
charge
potential
capacitance
current
The correct Answer is:D
To find the dimensions of the expression ϵ0dΦEdt, we will break it down step by step.
Step 1: Understand the terms involved
- ϵ0 is the permittivity of free space.
- ΦE is the electric flux.
- dΦEdt represents the rate of change of electric flux with respect to time.
Step 2: Find the dimensions of ϵ0
The permittivity of free space ϵ0 has dimensions given by:
(ϵ0)=(C2)(N⋅m2)
Where:
- (C) is the dimension of charge.
- (N) (Newton) can be expressed as (kg⋅m/s2).
Thus, we can rewrite the dimensions of ϵ0:
(ϵ0)=(C2)(kg⋅m/s2)⋅(m2)=(C2)(kg⋅m3/s2)=(C2⋅s2/(kg⋅m3))
Step 3: Find the dimensions of electric flux ΦE
Electric flux ΦE is defined as:
ΦE=E⋅A
Where:
- E is the electric field with dimensions (E)=(V)(m)=(J/C)(m)=(kg⋅m2/(s2⋅C))(m)=(kg⋅m)(s2⋅C).
- A is the area with dimensions (A)=(m2).
Thus, the dimensions of electric flux ΦE are:
(ΦE)=(E)⋅(A)=((kg⋅m)(s2⋅C))⋅(m2)=(kg⋅m3)(s2⋅C)
Step 4: Find the dimensions of dΦEdt
The rate of change of electric flux with respect to time has dimensions:
(dΦEdt)=(ΦE)(T)=(kg⋅m3/(s2⋅C))(s)=(kg⋅m3)(s3⋅C)
Step 5: Combine the dimensions
Now we can find the dimensions of the entire expression ϵ0dΦEdt:
(ϵ0dΦEdt)=(ϵ0)⋅(dΦEdt)
Substituting the dimensions we found:
=(C2⋅s2kg⋅m3)⋅(kg⋅m3s3⋅C)
When we multiply these, we get:
=C2⋅s2⋅kg⋅m3kg⋅m3⋅s3⋅C=C⋅s2s3=Cs=(I)
Where (I) is the dimension of electric current (Ampere).
Final Answer
The dimensions of ϵ0dΦEdt are the same as that of electric current, which is (I).
- ϵ0 is the permittivity of free space.
- ΦE is the electric flux.
- dΦEdt represents the rate of change of electric flux with respect to time.
The permittivity of free space ϵ0 has dimensions given by:
(ϵ0)=(C2)(N⋅m2)
Where:
- (C) is the dimension of charge.
- (N) (Newton) can be expressed as (kg⋅m/s2).
(ϵ0)=(C2)(kg⋅m/s2)⋅(m2)=(C2)(kg⋅m3/s2)=(C2⋅s2/(kg⋅m3))
Electric flux ΦE is defined as:
ΦE=E⋅A
Where:
- E is the electric field with dimensions (E)=(V)(m)=(J/C)(m)=(kg⋅m2/(s2⋅C))(m)=(kg⋅m)(s2⋅C).
- A is the area with dimensions (A)=(m2).
(ΦE)=(E)⋅(A)=((kg⋅m)(s2⋅C))⋅(m2)=(kg⋅m3)(s2⋅C)
The rate of change of electric flux with respect to time has dimensions:
(dΦEdt)=(ΦE)(T)=(kg⋅m3/(s2⋅C))(s)=(kg⋅m3)(s3⋅C)
Now we can find the dimensions of the entire expression ϵ0dΦEdt:
(ϵ0dΦEdt)=(ϵ0)⋅(dΦEdt)
Substituting the dimensions we found:
=(C2⋅s2kg⋅m3)⋅(kg⋅m3s3⋅C)
When we multiply these, we get:
=C2⋅s2⋅kg⋅m3kg⋅m3⋅s3⋅C=C⋅s2s3=Cs=(I)
Where (I) is the dimension of electric current (Ampere).
The dimensions of ϵ0dΦEdt are the same as that of electric current, which is (I).
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Check point 8.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec A
51 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Examples
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
Similar Questions
Knowledge Check
Dimensions of ε0dϕEdt are same as that of
A[AT]B[A]C[ML2T−2]D[ML−1T−2]The dimension of ε0dϕEdt is same as the dimension of
AchargeBcapacitanceCpotentialDcurrentIf E = energy , G= gravitational constant, I=impulse and M=mass, then dimensions of GIM2E2 are same as that of
AtimeBmassClengthDforce
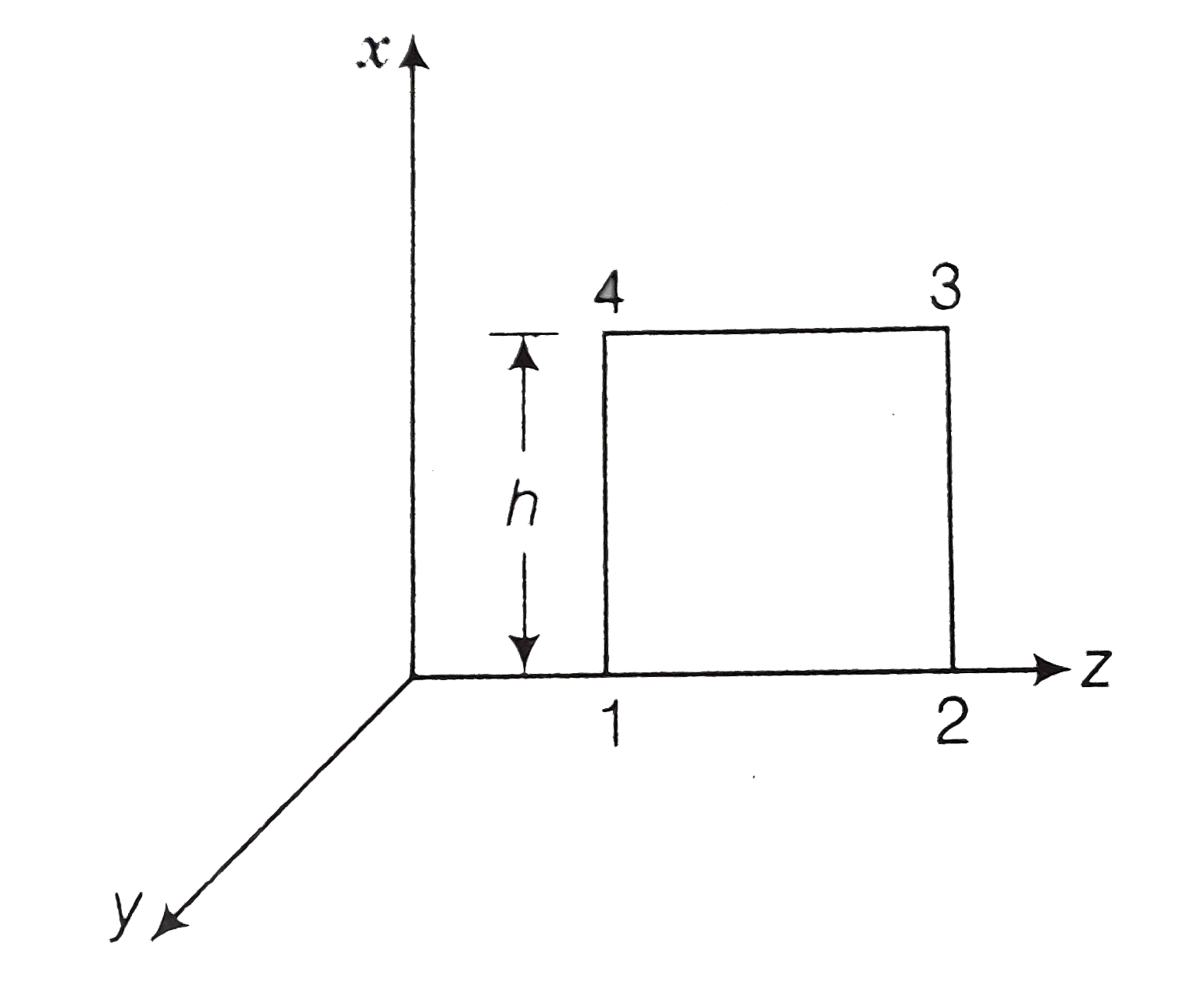
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
View SolutionIf E = energy , G= gravitational constant, I=impulse and M=mass, then dimensions of GIM2E2 are same as that of
View SolutionThe dimensions of velocity gradient are the same as that of
View SolutionThe dimension of 1√μ0ε0 are same as
View SolutionThe maxwell’s equation :
∮→B.→dl=μ0(i+ɛ0.dϕEdt) is a statement of -
View Solution
