Discuss the motion of a car on a banked road.
Step-by-Step Solution:
1. Understanding Banked Roads:
- A banked road is designed with an incline or tilt towards the center of the curve to help vehicles navigate turns more safely and efficiently. The angle of the bank is denoted as θ.
2. Forces Acting on the Car:
- When a car is on a banked road, several forces act on it:
- Weight (mg): Acts vertically downwards.
- Normal Force (R): Acts perpendicular to the surface of the road.
- Centripetal Force (mv²/r): Required for circular motion, directed towards the center of the curve.
- Frictional Force (F_r): Acts parallel to the surface of the road, opposing the motion down the slope.
3. Resolving Forces:
- The forces can be resolved into components:
- The centripetal force can be resolved into two components:
- mv2/r⋅cos(θ) (perpendicular to the road)
- mv2/r⋅sin(θ) (parallel to the road)
- The weight can also be resolved:
- mg⋅cos(θ) (perpendicular to the road)
- mg⋅sin(θ) (parallel to the road)
4. Setting Up Equations:
- For vertical forces (perpendicular to the road):
R=mgcos(θ)+mv2rsin(θ)
- For horizontal forces (parallel to the road):
mgsin(θ)=Fr+mv2rcos(θ)
- The frictional force can be expressed as Fr=μR.
5. Substituting and Simplifying:
- Substitute R from the first equation into the second:
mgsin(θ)=μ(mgcos(θ)+mv2rsin(θ))+mv2rcos(θ)
- Cancel m from all terms:
gsin(θ)=μgcos(θ)+μv2rsin(θ)+v2rcos(θ)
6. Rearranging the Equation:
- Rearranging gives:
gsin(θ)−μgcos(θ)=v2r(μsin(θ)+cos(θ))
- Solving for v2:
v2=r(gsin(θ)−μgcos(θ))μsin(θ)+cos(θ)
7. Finding the Velocity:
- Taking the square root gives the velocity:
v=√r(gsin(θ)−μgcos(θ))μsin(θ)+cos(θ)
8. Special Cases:
- No Friction: If μ=0:
v=√rgtan(θ)
- No Banking: If θ=0:
v=√rg−μg
- A banked road is designed with an incline or tilt towards the center of the curve to help vehicles navigate turns more safely and efficiently. The angle of the bank is denoted as θ.
- When a car is on a banked road, several forces act on it:
- Weight (mg): Acts vertically downwards.
- Normal Force (R): Acts perpendicular to the surface of the road.
- Centripetal Force (mv²/r): Required for circular motion, directed towards the center of the curve.
- Frictional Force (F_r): Acts parallel to the surface of the road, opposing the motion down the slope.
- The forces can be resolved into components:
- The centripetal force can be resolved into two components:
- mv2/r⋅cos(θ) (perpendicular to the road)
- mv2/r⋅sin(θ) (parallel to the road)
- The weight can also be resolved:
- mg⋅cos(θ) (perpendicular to the road)
- mg⋅sin(θ) (parallel to the road)
- For vertical forces (perpendicular to the road):
R=mgcos(θ)+mv2rsin(θ)
- For horizontal forces (parallel to the road):
mgsin(θ)=Fr+mv2rcos(θ)
- The frictional force can be expressed as Fr=μR.
- Substitute R from the first equation into the second:
mgsin(θ)=μ(mgcos(θ)+mv2rsin(θ))+mv2rcos(θ)
- Cancel m from all terms:
gsin(θ)=μgcos(θ)+μv2rsin(θ)+v2rcos(θ)
- Rearranging gives:
gsin(θ)−μgcos(θ)=v2r(μsin(θ)+cos(θ))
- Solving for v2:
v2=r(gsin(θ)−μgcos(θ))μsin(θ)+cos(θ)
- Taking the square root gives the velocity:
v=√r(gsin(θ)−μgcos(θ))μsin(θ)+cos(θ)
- No Friction: If μ=0:
v=√rgtan(θ)
- No Banking: If θ=0:
v=√rg−μg
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (SHORT ANSWER QUESTIONS)
Explore 33 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (VERY SHORT ANSWER QUESTIONS)
Explore 7 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
Explore 11 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
Select the correct equation for optimum speed of a car on a banked road of angle of banking θ and radius of curvature r.
View SolutionConsider the situation given in (Fig. 5.71). Two cars are moving along road 1 and 2. Draw the direction of the motion of
(a) Car B as seen from car A.
(b) Car A as seen from car B.
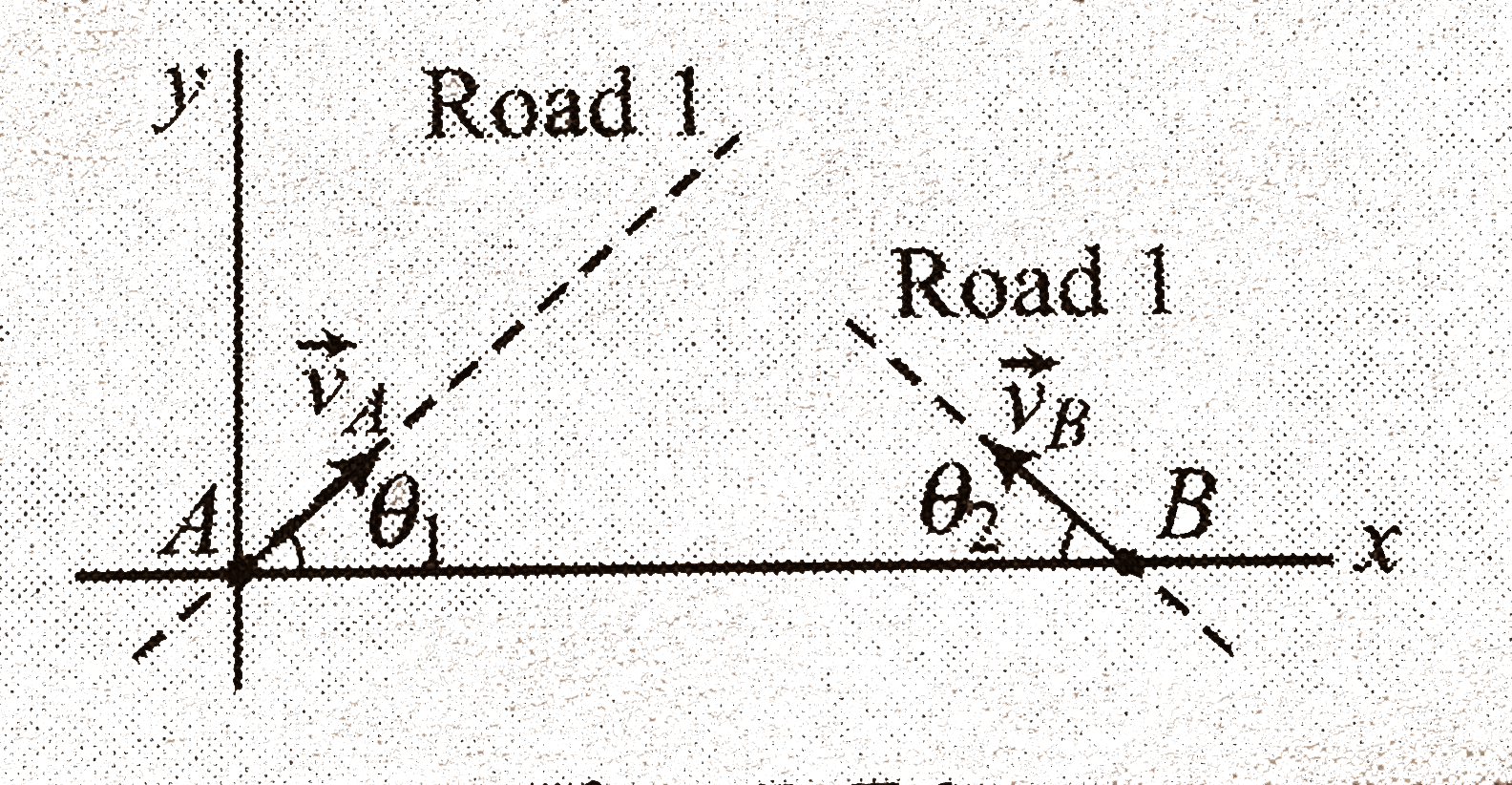 .
.
View SolutionTwo roads interest at right angle , one goes along the x - axis, another along the y - axis. At any instant, two cars AbadB moving along yandx directions, respectively, meet at intersection. Draw the direction of the motion of car A as seen from car B.
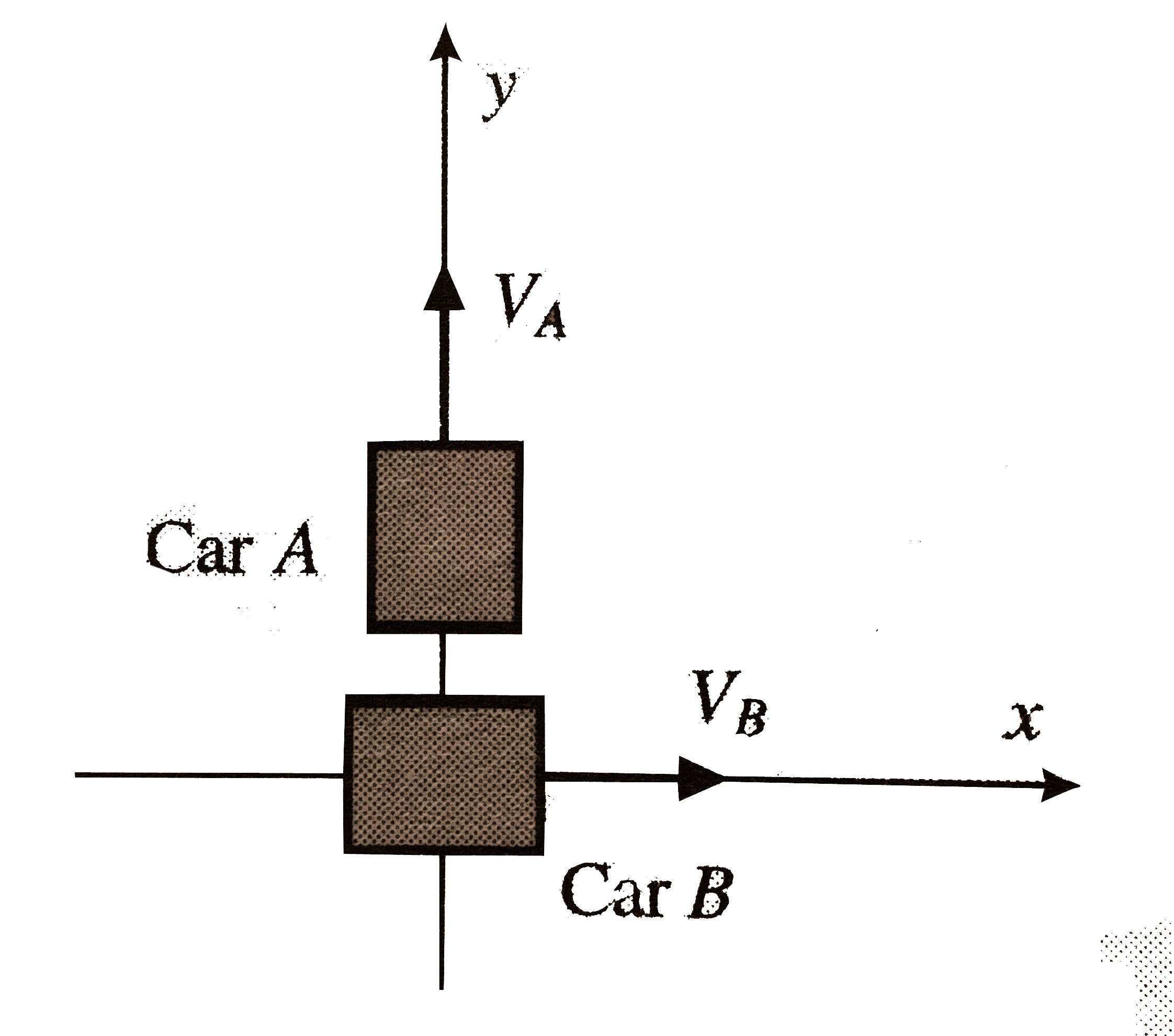 .
.
View Solution(A) : A maximum possible speed of a car on banked curved road is greater than that on a flat curved road
(R) : On a banked curved road horizontal component of normal reaction by road along with friction provides necessary centripetal force
View SolutionObtain an expression for the maximum speed with which a car can turn safely on a banked road.
View SolutionA car is moving along a banked road laid out as a circle of radius r . (a) What should be the banking angle θ so that the car travelling at speed v needs no frictional force from tyres to negotiate the turn ? (b) The coefficient of friction between tyres and road are μs=0.9 and μk=0.8 . At what maximum speed can a car enter the curve without sliding toward the top edge of the banked turn ?

View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
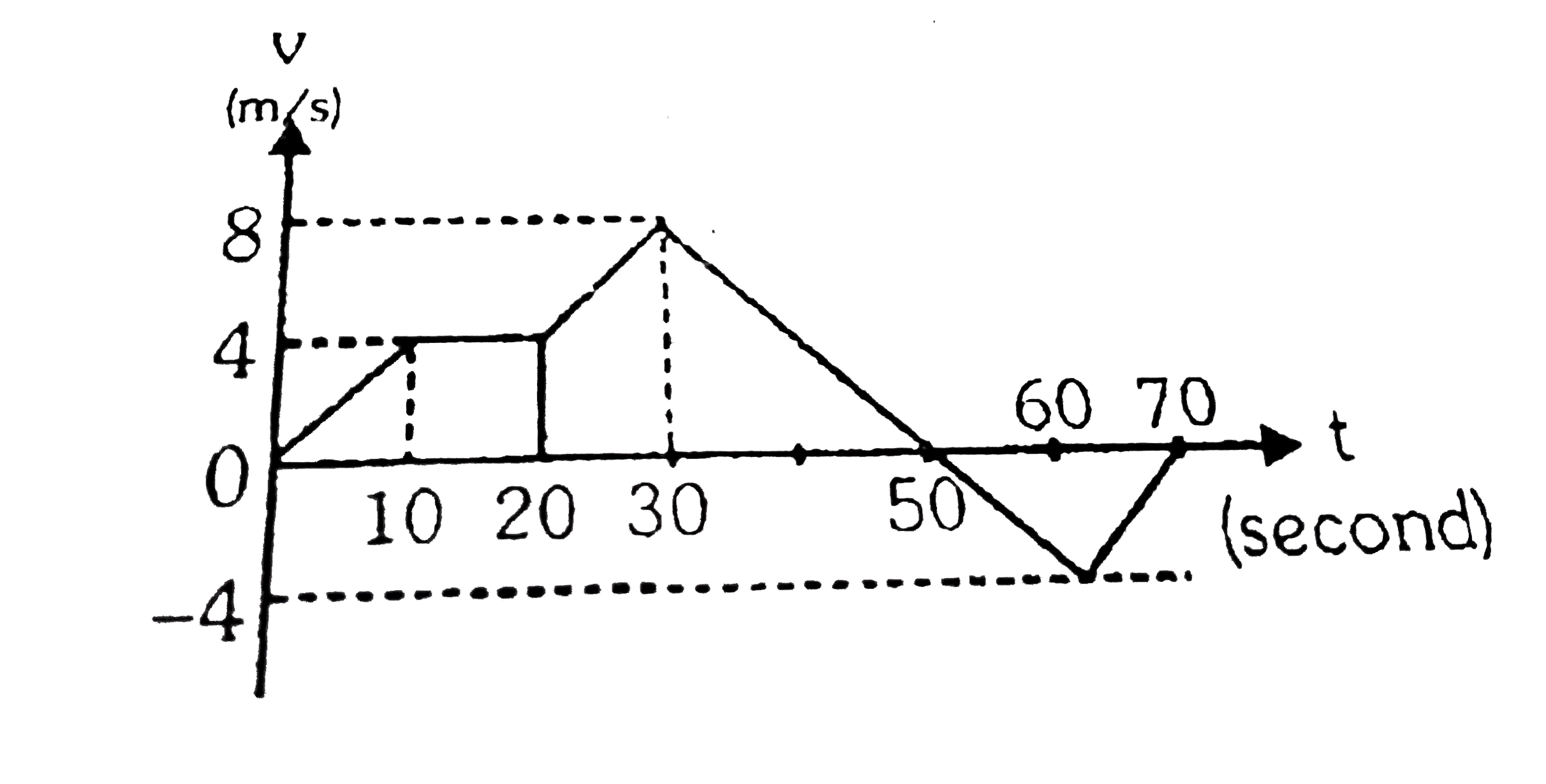
The maximum displacement from the starting position will be :-
View SolutionTwo roads one , along the y - axis and another along a direction at angle θ with x - axis, are as shown in (Fig. 5.68). Two cars AandB are moving along the roads. Considerthe situation of the diagram. Draw the direction of
(a) Car B as seen from car A.
(b) Car A as seen car B.
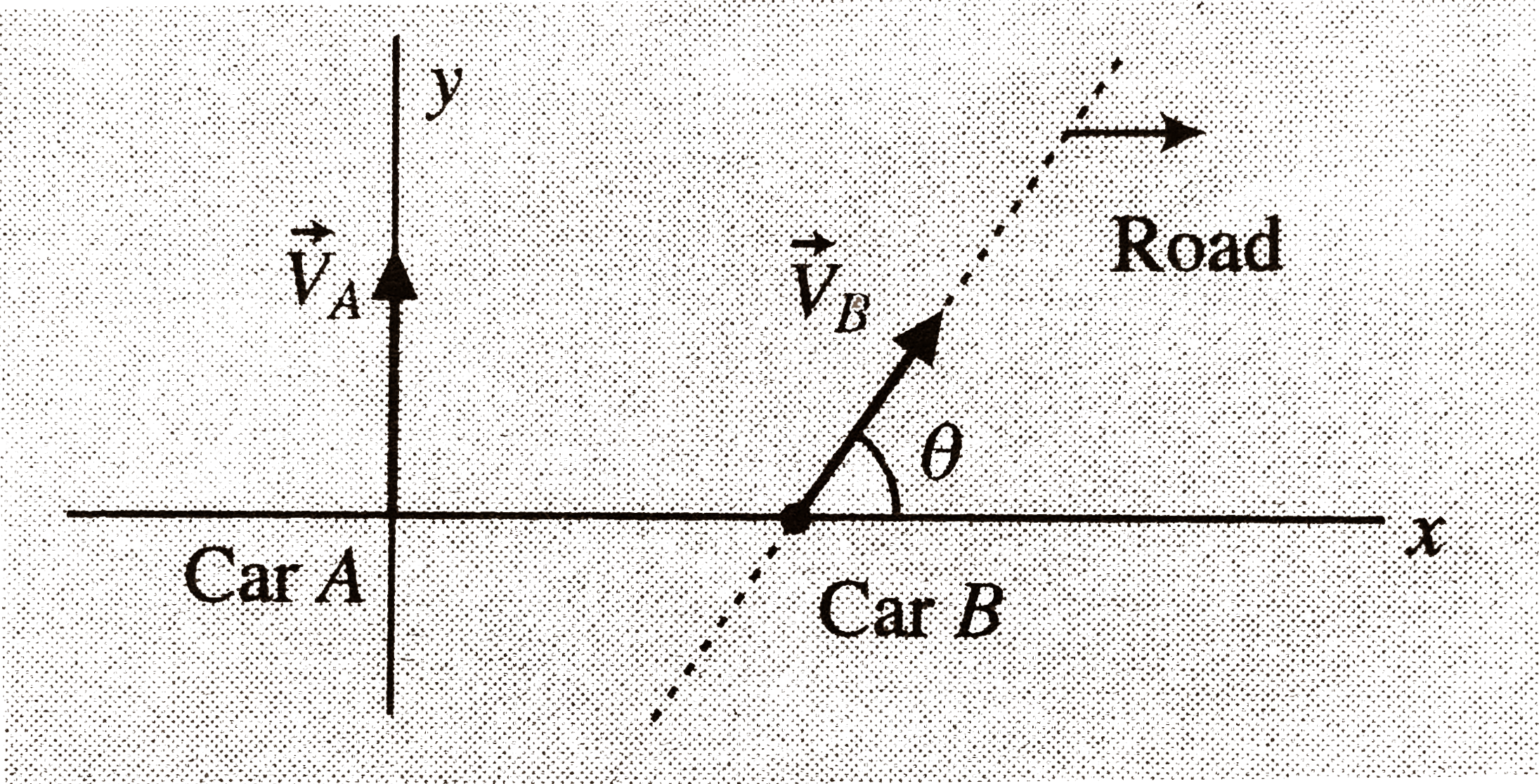 .
.
View SolutionA boy throws a ball in air at 60∘ to the horizontal along a road with a speed of 10m/s. Another boy sitting in a car passing by observes the ball. Sketch the motion of the ball as observed by the boy in the car, If car has a speed of (18km/h). Give explanation to support your diagram.
View SolutionA boy travelling in an open car moving on a levelled road with constant speed tosses a ball vetically up in the air and catches it back. Shetch the motion of the ball as observed by a boy stanceing on the footpath. Give explanation to support your diagram.
View Solution