Discuss the motion of charged particle in uniform magnetic field, when its moves at an angle θ with the direction of magnetic field. Prove that its path is helical. Calculate the pitch of helical path. What will be the nature of path if θ=90∘Solution in Punjabi
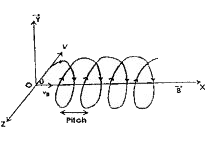
Let at any instant particle is moving with velocity v inside the uniform magnetic field →B making an angle θ with the direction of magnetic field.
Resolve →v into two rectangular components
(i) vB=vcosθ= the component of →v along the direction of magnetic field.
(ii) vn=vcosθ= the component of velocity →v normal to the direction of magnetic field.
As the magnetic field act perpendicular to the velocity component vn, the charged particle moves along a circular path.
As centripetal force is provided by magnetic force
∴Bqvn=mv2nr [vn is responsible for their motion in circular path]
r=mvnBq=mvsinθBq ...(i)
The period of the circular path is given by
T=2πrvn=2πvsinθ×mvsinθBq
or T=2πmBq ...(ii)
As the charged particle moves along circular path in XY-plane due to the velocity component vn, it also advances linearly along OZ due to the velocity component vB. As a result, the charged particle will move along the path as shown in Fig. Such a path is called helical path.
Pitch : The distance travelled by the charged particle. along the direction of magnetic field in a time it completes one revolution. is called pitch of the helical path. Therefore
Pitch of the helical path =vB×T=vcosθ×2πmBq
Pitch =2πmvcosθBq
Pitch of the helical path is equal to the spacing between its two consecutive circular paths
(i) if θ=90∘ i.e., when charged particle moves in a direction perpendicular to the direction of magnetic field (→B) then
r=mvsin90Bq
r=mvBq
vB=vcos90∘=0
It means that charged particle moves in a circular path.
(ii) If θ=180∘ then F F=Bqvsin180∘=0. Magnetic force acting on the charged particle ix zero and hence it will continue to move along the same path antiparallel to →B with same velocity →v .
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - NUMERICAL PROBLEMS14videos
FORCE ON A CHARGE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - SHORT ANSWER TYPE QUESTIONS (MOST EXPECTED QUESTIONS)3videos
FORCE ON A CHARGE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - NUMERICAL PROBLEMS (MOST EXPECTED QUESTIONS)6videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CURRENTEXERCISE - NUMERICAL PROBLEMS10videos
FORCE ON A CURRENT
Similar Questions
An electron (with charge 1.6×10−19C) moving at right angles to a uniform magnetic field completes a circular orbit in 10−6sec. Calculate the vlaue of magnetic field. Given mass of electron =9×10−31kg.
02:43View SolutionAn electron and a proton moving with same speed enter the same magnetic field region at right angles to the direction of the field. For which of the two particles will the radius of the circular path be smaller?
01:22View SolutionCalculate the electric potential at the surface of a gold nucleus. Given radius of nucleus = 6.6×10−15m and atomic wight of gold is 79.
02:13View SolutionA currentof 5.0 A is flowing in eah of the two parallel conductors of infinite length separated by certain distance apart in vacuum in the same directions. Each conductor expereinces a force of 2×10−4Nm−1 due to the other. Find the separation between the two conductors.
04:23View SolutionA charged particle enters a uniform magnetic field with velocity vector at angle of 45∘ with the magnetic field. The pitch of the helical path followed by the particle is p. the radius of the helix will be
04:39View SolutionAn electron is projected at an angle θ with a uniform magnetic field. If the pitch of the helical path is equal to its radius, then the angle of projection is
14:09View SolutionA charged particle is fired at an angle theta to a uniform magnetic field directed along the x-axis. During its motionalong a helical path, the particle will
36:40View SolutionA charged particle is fired at an angle θ to a uniform magnetic field directed along the x−axis. During its motion along a helical path, if the pitch of the helical path is equal to the maximum distance of the particle from the x− axis
08:56View SolutionA charged particle is fired at an angle "theta" to a uniform magnetic field directed along the "x" -axis.The resulting pitch of the helical path of the particle is equal to the maximum distance of the particle from the "x" -axis. The value of "theta" is?
05:18View SolutionMagnetism (Circular and Helical Motion)|Variation of Path of a Charged Particle in Uniform Magnetic Field
01:47View SolutionHelical Path of a Charged Particle Inside Magnetic Field
06:12View SolutionDiscuss the motion of charged particle in uniform magnetic field, when its moves at an angle theta with the direction of magnetic field. Prove that its path is helical. Calculate the pitch of helical path. What will be the nature of path if theta=90^@
02:38View SolutionDiscuss the motion of a charged particle in uniform magnetic field, when it moves at an angle 0 with the direction of magnetic field. Prove that its path is helical.Calculate the pitch of the helical path.What will be the nature of the path, if (i) θ=0∘and(ii)θ=180∘ ?
09:00View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
02:39View SolutionDiscuss the motion of charged particle in uniform magnetic field, when its moves at an angle theta with the direction of magnetic field. Prove that its path is helical. Calculate the pitcg of helical path. WHat will be the nature of path if theta=180^@
View SolutionAn electron is projected at an angle θ with a uniform magnetic field. If the pitch of the helical path is equal to its radius, then the angle of projection is
View Solution

