Discuss the phenomenon of refraction of light through a glass prism. Derive the relation: $A + δ = i + e$ ,where the symbols have their usual meninges.Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

Let abc is the principal section of a glass prism with angle A as angle of prism. Sides AB and AC are called refracting edges of the prms. Let a ray of light XY is incident on AB at the point Y. This ray will get refracted along YZ and finally emerge out along ZW. Draw TYM perpendicular on AB at Y and MZN on AC at Z. Produce XY forward and WZ backward.

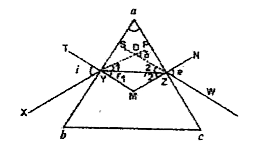
Now $∠ T Y H X = i =$ Angle of incidence
$∠ N Z W = e =$ Angle of emergence
$∠ Z Y M = r_{1} =$ Angle of refraction
$∠ Y Z M = r_{2} =$ Angle of refraction
$∠ S D Y = ∠ P D Z = δ =$ angle of deviation
$∠ B A C = A =$ Angle of prism
Now $∠ 1 + i - r_{1}$ and $∠ 2 = e - r_{2}$ .............2
In triangle $Y Z M, r_{1} + r_{2} = ∠ M = 180^{\circ}$
Also in quadrilaeral AYMZ $∠ A + ∠ M = 180^{\circ}$ ..........3
Comparing eqn 2 and 3
$∠ A + ∠ M = r_{1} + r_{2} + ∠ M$
$∴ ∠ A = r_{1} + r_{2}$
Now in triangle $Y Z D δ = ∠ 1 + ∠ 2$
Substituting the vaues of $∠ 1$ and $∠ 2$ from eqn (1) we get
$δ = i - r_{1} + e - r_{2}$
$= i + e - (r_{1} + r_{2})$
Substituting the values from eq. (4) in the above relation we get
$δ = i + e - A$
$δ + A = i + e$
$δ i + e - A$ ..........5
If $μ =$ Refractive index of the material of prism
By applying Snell.s law at point Y.
$μ = \frac{\sin i}{{\sin r}_{1}} = \frac{i}{r_{1}}$ (when angles are small then $\sin i = i$
and ${\sin r}_{1} = r_{1}$
$\Rightarrow i = μ r_{1}$
By applying law at point Z, we have
$\frac{{\sin r}_{2}}{\sin e} =^{g} μ_{a} = \frac{1}{^{a} μ_{g}}$
and $\frac{1}{μ} = \frac{r_{2}}{}$ (when angles are small then ${\sin r}_{2} = r_{2}$
and $\sin e = e$ )
$\Rightarrow e = μ_{2}$
Put value of i and e in eqn (5)
$δ = μ r_{1} + μ r_{2} - A = μ (r_{1} + r_{2}) - A$
$δ = μ A - A$ [using eqn (4)]
$δ = (μ - 1) A$
This is the angle through which light ray deviates on passing through prism of small angle A.

|

Updated on:21/07/2023

Class 12 PHYSICS DIPERSION OF LIGHT

Topper's Solved these Questions

Similar Questions

BETTER CHOICE PUBLICATION-DIPERSION OF LIGHT-LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile