Drift speed of electron inside the metallic conductor is vA=eEymzτ (here, e= electronic charge, E= electric field, m= mass of electron and τ= time relaxation). Find the value of y.
32
0
12
1
The correct Answer is:d
The unit of LHS =m1s−1
The unit of RHS
=coulomb(newtoncolomb)1(kilogram)2(second)
But The unit of LHS= unit of RHS
Colomb does not come in RHS
(colomb1(colomb)2)= unitless
⇒y=1
Topper's Solved these Questions
Similar Questions
Knowledge Check
The angular momentum of electron is J. if e=charge of electron , m= mass of electron , then its magnetic moment will be
AmJ2eBeJ2mC2meJDemJ2.The em value of electron is
A1.76×10−11ckg−1B1.76×1011ckg−1C1.76×1012kg−1cD1.76×1013kg−1cDrift speed vd of electrons in a conductor varies with the strength of electric field E as per the relation :
Avd∝EBvd∝1ECvd∝E2Dvd does not depends on E
(a) Write the nature of path of free electrons in a conductor in the (i) presence of electric field (ii) absence of electric field.
(b) Between two successive collisions each free electron acquires a velocity from 0 to v where v=eEmτ. What is the average velocity of a free electron in the presence of an electric field.
View SolutionFind the expression of radius of an orbit of electron in terms of nucleus charge Q2, tangential velocity v and mass of electron me ?
View SolutionWhen electric field inside a conductor is E, mobility of free electrons inside the conductor is μ. When the electric field is doubled mobility will be
View SolutionAn electron having charge 'e' and mass 'm' is moving a uniform electric field E. Its acceleration will be
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
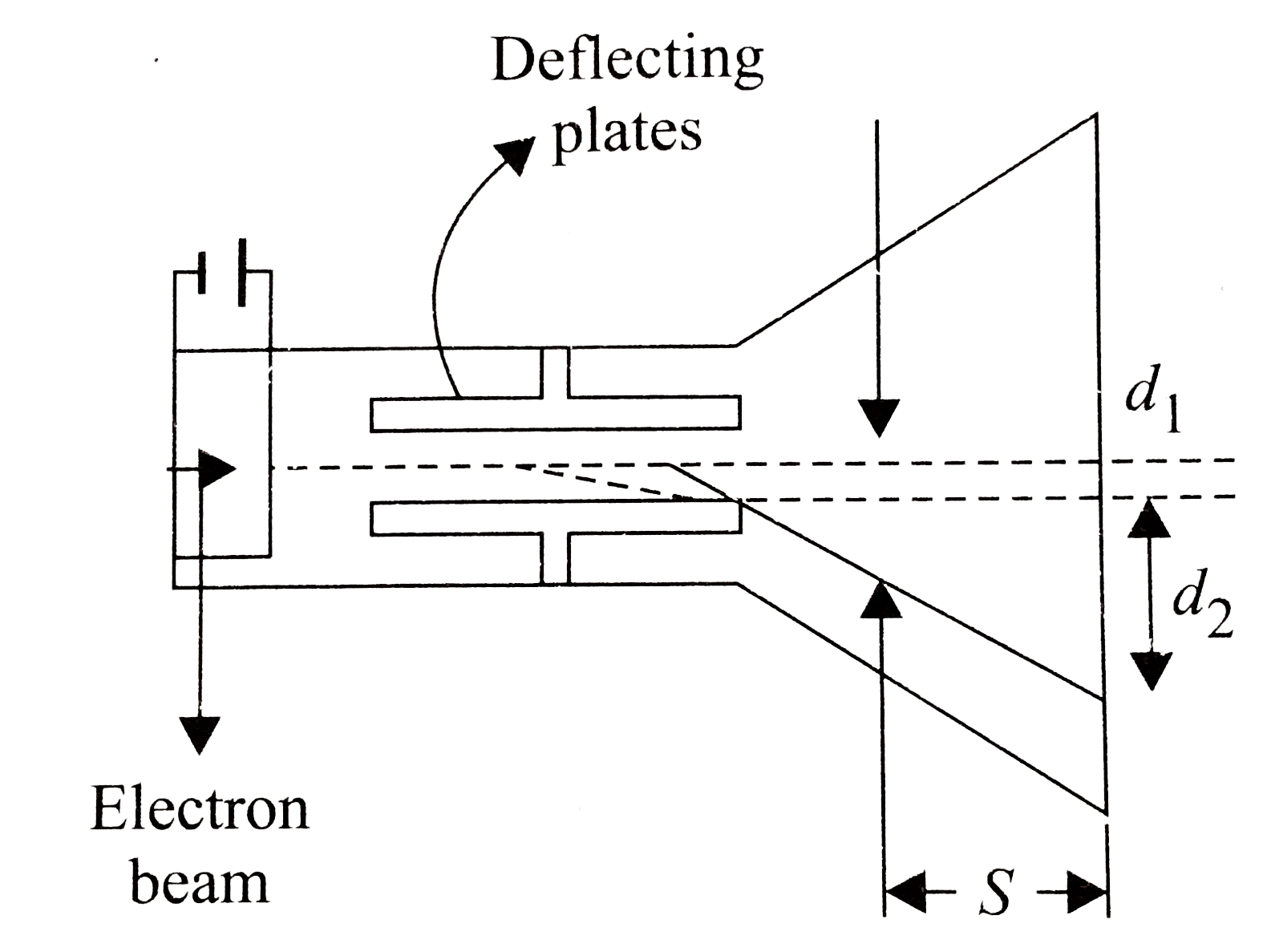
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
View Solution
