
Eleven identical rods are arranged as shown in Fig. Each rod has length l, cross sectional area A and thermal conductivity of material L. Ends A and F are maintained at temperatures T1 and T2(<T1), respectively. If lateral surface of each rod is thermally insulated, the rate of heat transfer (dQdt) in each rod is
(dQdt)AB=(dQdt)CD
(dQdt)BE=27(T1−T2)KAl
(dQdt)CH≠(dQdt)DG
(dQdt)BC=(dQdt)DC
The correct Answer is:B, C, D
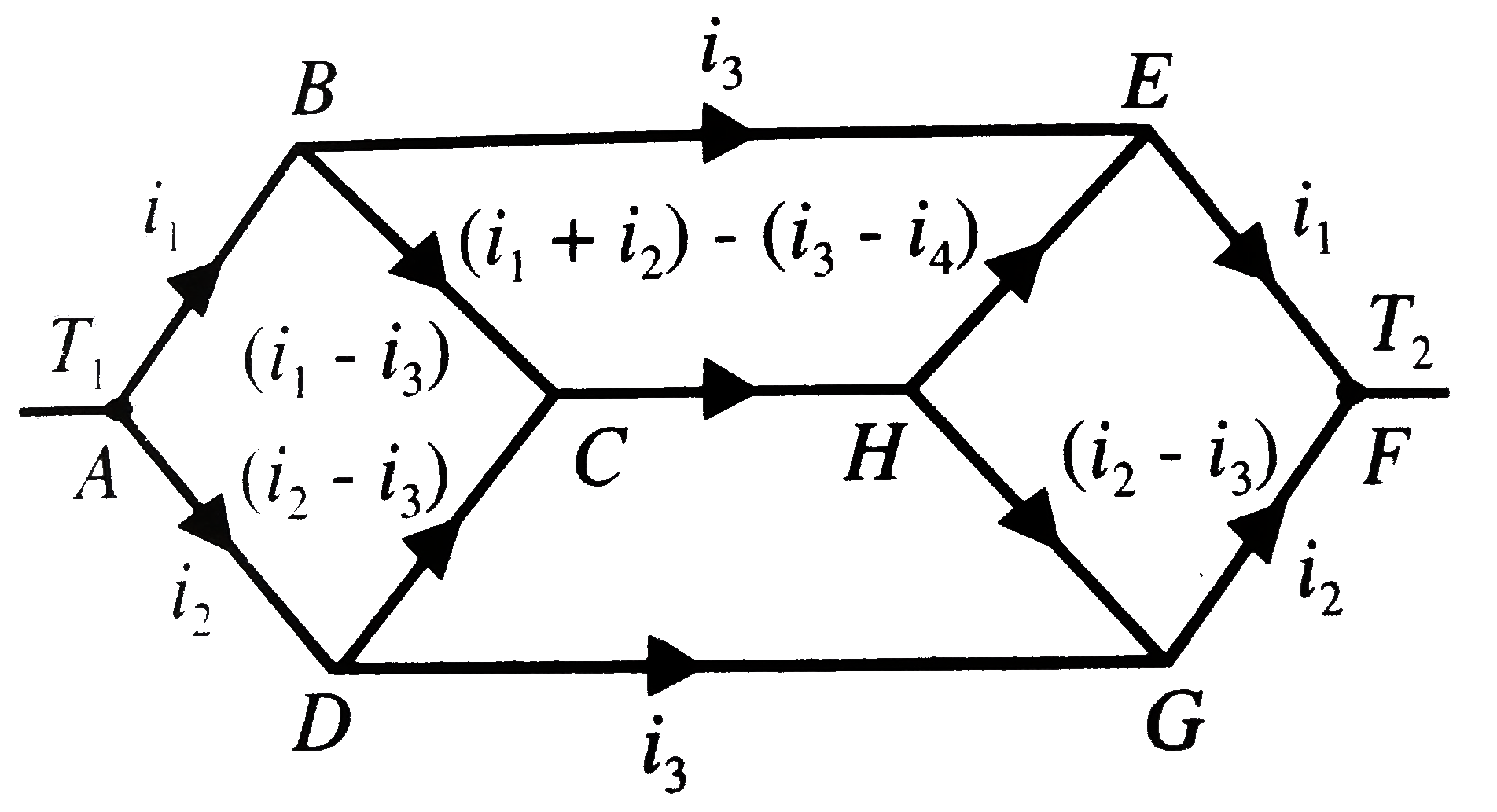
Resistance of each rod R=lkA
In steady state TB=TD
TE=TG
Thermal current (dQdt)=i
i1R+i3R+i1R=(T1−T2)
2i1+i3=(T1−T2)R ..(i)
2i1+i3=T1−T2R .(ii)
i1=i2
For the path ABCHGF
i1R+(i1−i3)R+2(i1+i3)R+(i1−i3)R+i1R=(T1−T2)
6ii−4i3=(T1−T2)R=2ii+i3 .(iv)
4ii=5i3⇒i3=45ii .(v)
From eqs (ii) and (v)
2ii+45i1=(T1−T2)R
14ii5=(T1−T2)R
Equivalent thermal resistance (T1−T2)2ii=75R
(dQdt)AB=i1=5(T1−T2)KA14l
(dQdt)BE=27(T1−T2)KAl
(dQdt)BC=(T1−T2)KA14l
(dQdt)CH=(T1−T2)KA7l

Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Integer
8 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Single Correct
148 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
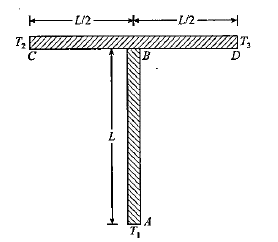
Four identical rods AB,CD,CFandDE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l,AandK respectively. The ends A,EandF are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
View Solution
Knowledge Check
Cylinder copper rod of length 1m and a cylinder steel rod of length 1.5m are joined together end to end. The cross sectional area of eac rod is 3.14cm. The free ends of steel rod and copper rods are maintained at 0∘C and 100∘C respectively. The surfaces of rods are thermally insulated. Find the temperature of copper steel junction. (Given thermal conductivity of steel =46J/m−s.∘C and the thermal conductivity of copper =386J/m−s.∘C)
A40∘B60∘C93∘D80.64∘CFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
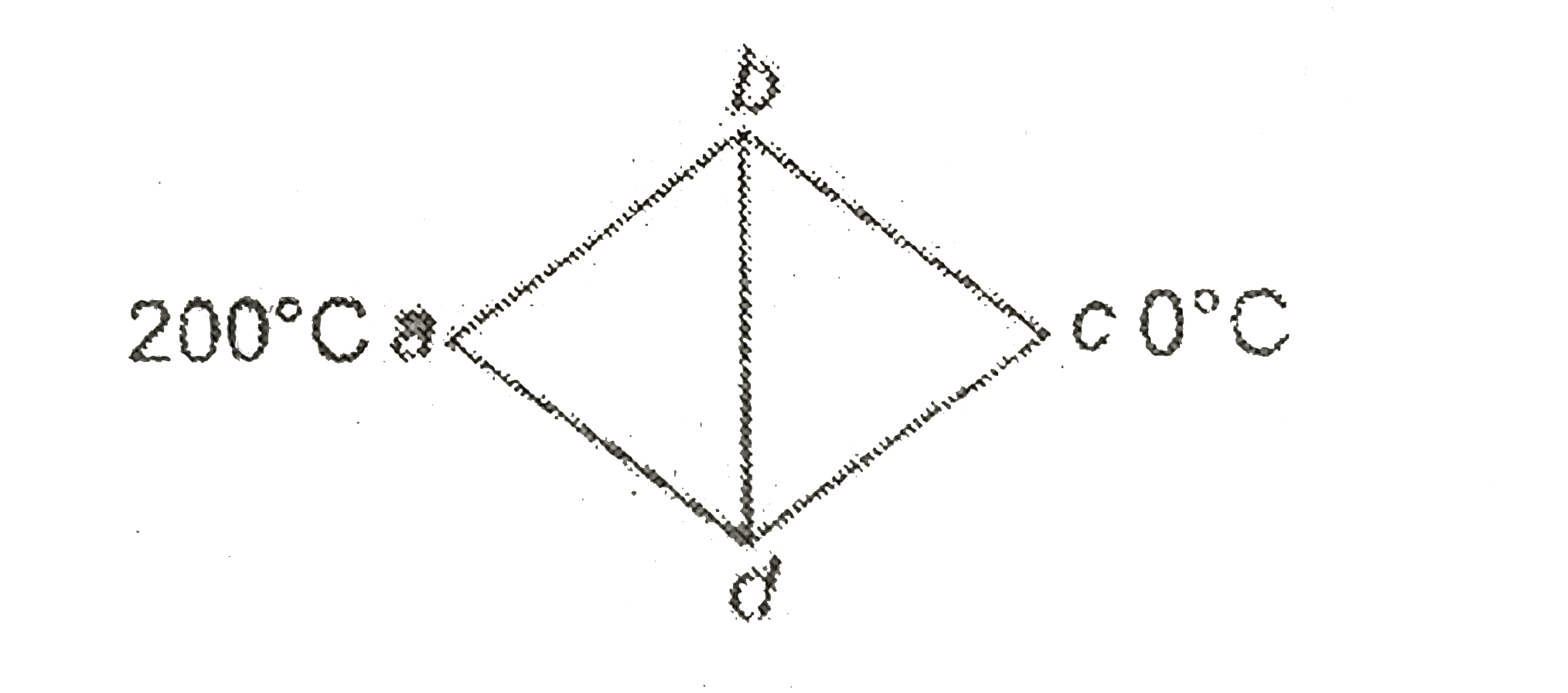
For what length x of rod dc there will be no heat flow through rod bd ?A4lB2lC6lD9lA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
AAαT21−T22lBAαT21+T22lCAαT21+T223lDAαT21−T222l
Four identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmospere, find the temperature at B.

View SolutionFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.

For what length x of rod dc there will be no heat flow through rod bd ?
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
