Establish the following inequalities geometrically or otherwise ,
(a) $∣ ∣ \to A + \to B ∣ ∣ \leq ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$ ,
(b) $∣ ∣ \to A + \to B ∣ ∣ \geq ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$
(C ) $∣ ∣ \to A - \to B ∣ ∣ \leq ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
(d) $∣ ∣ \to A - \to B ∣ ∣ \geq ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$
When does the equality sign above apply ?

Text Solution

Verified by Experts

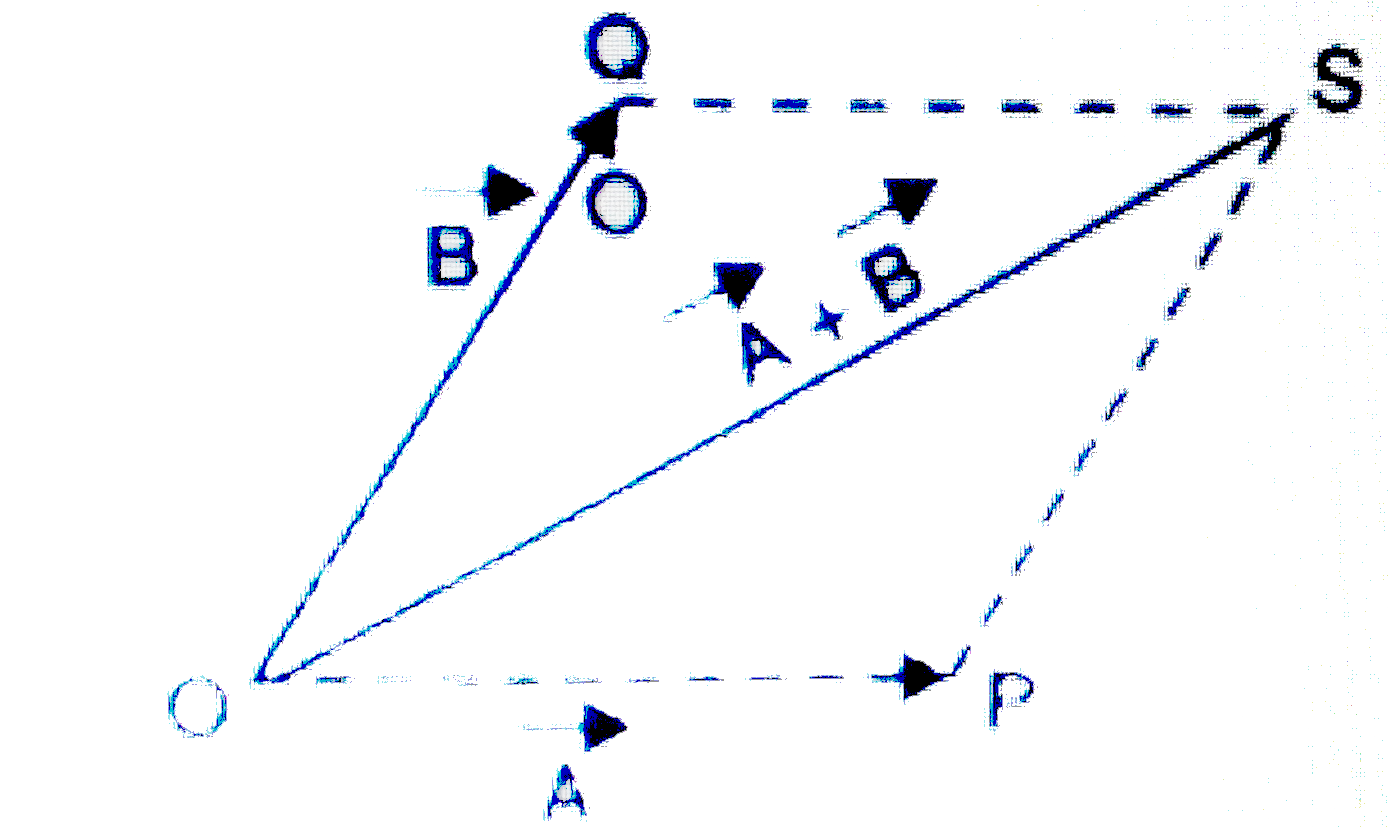
Consider two vectors $\to A$ and $\to B$ be represented by the sides $- - \to O P$ and $- - \to O Q$ of a parallelogram OPSQ. According to parallelogram law of vector addition, $(\to A + \to B)$ will be represented by $- - \to O S$ as shown in Fig. Thus,
OP = $∣ ∣ \to A ∣ ∣$ , $O Q = P S = ∣ ∣ \to B ∣ ∣$
and OS = $| v e r A + v e r B |$
a) To prove $∣ ∣ \to A + \to B ∣ ∣ \leftarrow ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
We know that the length of one side of a triangle is always less than the sum of the lengths of the other two sides. Hence from $Δ$ OPS, we have,
OSltOP+PS or OSltOP+OQ or $∣ ∣ \to A + \to B ∣ ∣ < ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$ ..............(i)
If the two vectors $\to A$ and $\to B$ are acting along the same straight line and in the same direction
then, $∣ ∣ \to A + \to B ∣ ∣ = ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$ ..............(ii)
Combining the conditions mentioned in (i) and (ii) we have
$∣ ∣ \to A + \to B ∣ ∣ \leftarrow ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
b) To prove $∣ ∣ \to A + \to B ∣ ∣ > - ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$
From $Δ$ OPS, we have $O S + P S > O P$ or $O S > | O P - P S |$ or $O S > | O P - O Q |$ ............(iii) $(∴$ PS=OQ)
The modules of (OP-PS) has been taken because the L.H.S is always positive but the R.H.S may be negative if $O P < P S$ . thus from (iii) , we have,
$∣ ∣ \to A + \to B ∣ ∣ > ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$ .............(iv)
if the two vectors $\to A$ and $\to B$ are acting along a straight line in opposite directions, then
$∣ ∣ \to A + \to B ∣ ∣ = ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$ ............(v)
Combining the conditions mentioned in (iv) and (v), we get
$∣ ∣ \to A + \to B ∣ ∣ \geq ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$
c) To prove $∣ ∣ \to A - \to B ∣ ∣ \leq ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
In fig. $\to O L$ and $- - \to O M$ represents vectors $\to A$ and $\to B$ respectively. Here $- - \to O N$ represents $- --- \to A - B$ .
consider the $Δ$ OMN,
$O N < M N + O M$
$∣ ∣ \to A - \to B ∣ ∣ < ∣ ∣ \to A ∣ ∣ + ∣ ∣ - \to B ∣ ∣$ ............(vi)
When $\to A$ and $\to B$ are along the same line, but points in the opposite direction, then
When $\to A$ and $\to B$ are along the same straight line, but points in the opposite direction, then
$∣ ∣ \to A - \to B ∣ ∣ = ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$ ............(vii)
combining equation (vi) and (vii), we get
$∣ ∣ \to A - \to B ∣ ∣ \leftarrow ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
d) To prove $∣ ∣ \to A - \to B ∣ ∣ \leq ∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
Let us consider the $Δ O M N$ ,
$O N + O M > M N$ or $O N > [M N - O M]$
since, $M N = O L$ $∴$ $O N > | O L - O M |$
or $∣ ∣ \to A - \to B ∣ ∣ > ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$ ...................(viii)
When $\to A$ and $\to B$ are along the same straight line and point in the same direction,then
$∣ ∣ \to A - \to B ∣ ∣ = ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣$ ............(ix)
Combining equations (viii) and (ix), we get
$∣ ∣ \to A - \to B ∣ ∣ \geq ∣ ∣ ∣ ∣ \to A ∣ ∣ - ∣ ∣ \to B ∣ ∣ ∣$

Updated on:21/07/2023

|

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

NCERT ENGLISH-MOTION IN A PLANE -EXERCISE

Home
Ask Doubt
Profile