Evaluate 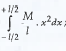 , where M and l are constants.
, where M and l are constants.
Step by step video & image solution for Evaluate , where M and l are constants. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
- LAWS OF MOTION : FRICTIONBOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Self Practice
95 Videos
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
Similar Questions
Find the value of
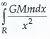 , where G,M and m are constants.
, where G,M and m are constants.
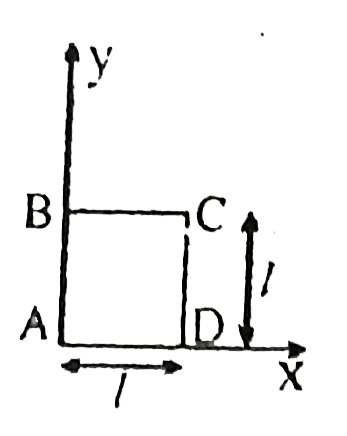
View SolutionA square loop of side 'l' each side having uniform linear charge density 'lambda' is placed in 'xy' lane as shown in the figure There exists a non uniform electric field →E=al(x+l)ˆi where a and l are constants and x is the position of the point from origin along x-axis. Find the resultant electric force on the loop (in Newtons) if l=10cmλ=20μC/manda=5×105N/C.
View Solution
Knowledge Check
If (x+a) is a factor of both the quadratic polynomials x2+px+qandx2+lx+m , where p,q,l and m are constants, then which one of the following is correct?
Aa=(m−q)/(l−p)(l≠p)Ba=(m−q)/(l+p)(l≠−p)Cl=(m−q)/(a−p)(a≠p)Dp=(m−q)/(a−l)(a≠l)Simplify:- 8059 - 7263 = ? * 40
Aa. 19.9Bb. 18.7Cc. 15.9Dd. 17.7
FInd the derivative by first principle ax+b where a and b are constants
View SolutionEvaluate ∫t_0Asinωdt where A and omega are constants.
View SolutionShow that the sequence defined by an=m+(2n−1) d, where m and d are constants , is an
A.P. Find its common difference .
View SolutionFind the derivative of 3sinx+2sinα, where 'α' is a constant.
View SolutionA particle moves along an arc of a circle of radius R according to the law l=asinωt, where l is the displacement from the initial position measured along the arc, and a and ω are constants. Assuming R=1.00m, a=0.80m, and ω=2.00rad/s, find:
(a) the magnitude of the total acceleration of the particle at the points l=0 and l=±a,
(b) the minimum value of the total acceleration wmin and the corresponding displacement lm.
View SolutionIf lx+my+n=0, where l,m,n are variables, is the equation of a variable line and l,m,n are connected by the relation al+bm+cn=0 where a,b,c are constants. Show that the line passes through a fixed point.
View Solution
