Question

Explain the working of simple microscope and find an expression for its magnifying power. What are the uses of simple microscope?

Explanation

A convex lens of short focal length can be used to see magnified image of a small object and is called a simple microscope.
Principle : When a small object is placed between optical centre and focus of a convex lens, its virtual, erect and magnified image is formed on the same side of the lens. The lens is held close to eye and the distance of the object is adjusted, till the image is formed at the least distance of distinct vision from the eye. For a normal eye, the least distance vision is 25 cm.
Working : Let AB be an object placed between the points F and C. Its virtual image A.B. will be formed on the same side of the object. If the distance of the object is changed from the lens, then the distance of the image also changes. The position of object AB is so adjusted that the image A.B. is formed at the least distance of distinct vision (D) as shown in Fig.

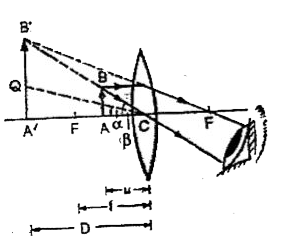
Magnifying power (When image is formed at D): It is defined as the ratio of the angle subtended by the image at the eye and the angle subtended by the object seen directly when both lie at the least distance of distinct vision. It is also called angular magnification produced by the simple microscope. It is denoted by M.
Let `angleA.CB. =beta` be the angle subtended by the image at the eye. Cut A.Q equal to AB and join QC. Then, `angleA.CQ=alpha` is the angle subtended by the object at the eye, when it is placed at the least distance of distinct vision.
By definition, magnifying power of the simple microscope is given by
`M=(beta)/(alpha)`
In practice, angles `alpha` and `beta` are small. Therefore, angles `alpha` and `beta` can be replaced by their tangents
i.e. `M=(tan beta)/(tan alpha)" " ...(i)`
From right angled `DeltaCA.Q, tan alpha=(AQ)/(CA)=(AB)/(CA)" " ( :. A.=AB)`
Also, from right angled `DeltaCAB, tan beta=(Ab)/(CA)`
Substituting for tan `alpha` and tan `beta` in equation (i), we have
`M=(AB//CA)/(AB//CA)" " ...(ii)`
If CA = u, the distance of object AB from the lens and CA. = y, the distance of image A.B. from the lens, then
`M=(v)/(u)" " ...(iii)`
If f is focal length of the lens acting as simple microscope, then
`-(1)/(u)+(1)/(v)=(1)/(f)`
Multiply both sides by v
`-(v)/(u)+(v)/(v)=(v)/(f)`
`-(v)/(u)+1=(v)/(f)`
or `(v)/(u)= 1-(v)/(f) " "....(iv)`
From equations (iii) and (iv), we have
`M= 1-(v)/(f)`
Applying new cartesian sign conventions L
`v= -D, f= +f`
`M= 1-((-D)/(+f))`
or `M=1+(D)/(f) " " ...(v)`
From equation (v), it follows that lesser is the focal length of the convex lens used as simple microscope, greater is the value of the magnifying power obtained.