Explain with the help of a labelled diagram the distribution of magnetic field due to a current through a circular loop. Why is it that if a current carrying coil has n turns, the field produced at any point is n times as large as that produced by a single turn?

Video Solution

Text Solution

Generated By DoubtnutGPT

To explain the distribution of the magnetic field due to a current flowing through a circular loop, we can follow these steps:
1. Understanding the Circular Loop:
- Consider a circular loop of wire through which an electric current (I) is flowing. The loop can be visualized as a flat circle.
2. Direction of Current:
- Assume the current flows in a clockwise direction when viewed from one side of the loop.
3. Applying the Right-Hand Rule:
- To determine the direction of the magnetic field produced by the current, we can use the right-hand rule. If you curl the fingers of your right hand in the direction of the current, your thumb will point in the direction of the magnetic field lines.
4. Magnetic Field Lines:
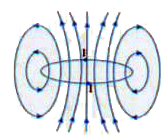
- At the center of the loop, the magnetic field lines will emerge from one side of the loop (the north pole) and enter the other side (the south pole). The magnetic field lines will form closed loops around the wire.
5. Labelled Diagram:
- Draw a circular loop and label the direction of the current (I), the north pole (N) where the field lines emerge, and the south pole (S) where the field lines enter. Indicate the magnetic field lines as arrows curling around the loop.
6. Magnetic Field Strength:
- The magnetic field (B) at the center of a single circular loop can be calculated using the formula:
$B = \frac{μ_{0} I}{2 R}$
where $μ_{0}$ is the permeability of free space, $I$ is the current, and $R$ is the radius of the loop.
7. Effect of Multiple Turns:
- If the loop has $n$ turns, the magnetic field at the center of the coil will be $n$ times stronger than that of a single loop. This is because each turn contributes to the total magnetic field in the same direction.
8. Final Formula for n Turns:
- The magnetic field for $n$ turns is given by:
$B_{n} = n \cdot \frac{μ_{0} I}{2 R} = \frac{n μ_{0} I}{2 R}$
- This shows that increasing the number of turns increases the magnetic field strength proportionally.
Conclusion
The magnetic field produced by a current-carrying circular loop can be visualized with the help of magnetic field lines. The strength of the magnetic field increases linearly with the number of turns in the coil, as each turn contributes to the total magnetic field at the center.
---

The magnetic field due to current carrying circular coil having n turns is
A $n^{2}$ times as large as that produced by a single turn
Bn times as large as that produced by a single turn
C $\frac{1}{2}$ -times as large as that produced by a single turn
Dwill be same as that produced by a single turn
The magnetic field produced due to a current through a circular loop depends directly on ............ .
Aradius of the loop
Bcurrent passing through it
Cresistance of the wire
Dthickness of the wire