Explain work done by torque. Solution in Gujrati
Suppose a rigid body rotating about a fixed axis, which is taken as the Z-axis. This axis is perpendicular to plane X.Y..
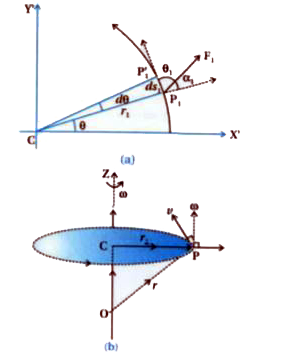
Let force −→F1 acting on a particle of the body at point P1 and it rotates on a circle of radius r1 with centre C on the axis CP1=r1.
In time Δt, the point moves to the position P.1 from P1. The displacement of the particle is ΔS1=r1Δθ and it is in the direction tangential at P1∴Δθ=∠P1OP.1 is the angular displacement of the particle. The work done by the force −→F1 on the particle is
dW1=−→F1.d→S1
=F1ΔS1cosϕ1
=F1r1Δθcos(90∘−α1)
where ΔS1=r1Δθandϕ1+α1=90∘
where ϕ1 is the angle between −→F1 and the tangent at P1andα1 is the angle between −→F1 and the radius vector −−→OP=→r1,ϕ
The torque due to −→F1 about the origin
→τ=−−→OP1×−→F1 ....(1)
but according to figure (b)
−−→OP1=−−→OC+−−→CP1
Since −−→OP is along the axis,
∴τ=OC(F1)sin0∘=0, hence −−→OP1=−−→CP1
From eqn. (1),
→τ1=−−→CP1×−→F1
∴→τ1=→r1×−→F1[∵−−→CP1=→r1]
∴τ1=r1F1sinα1
and work ΔW1=τ1Δθ
If there are more than one forces acting on the body the work done by all of them can be added to give the total work done on the body
ΔW=(τ1+τ2+τ3+....τn)Δθ
∴ΔW=τΔθ ....(2)
where τ1+τ2+τ3+....τn=τ total torque
If Δθ→0 total work done,
dW=τdθ is similar to eqn.
dW=Fds in linear motion
Diving (2) on both in eqn. (2)
ΔWΔt=τ.ΔθΔt
If Δt→0=ΔWΔt=dWdtandΔθΔt=dθdt
∴ Instantaneous power,
P=τ.dθdt
∴P=τω
This is the instantaneous power. It is similar to equation P=Fv in linear motion.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A HOTS
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A (TRY YOURSELF (VSQs))
94 Videos
- QUESTIONS ASKED IN JEE - 2020 BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
Similar Questions
What is torque? Explain the torque acting on a particle.
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionExplain negative value of work done.
View SolutionA torque of 103 Nm acting on a rigid body, turns it through 30° in 0.2 second. Calculate the work done by the torque on the body and power of torque.
View SolutionMention the SI unit of torque. Though dimensional formula of work and torque is the same, joule is not used to measure torque. Explain why ?
View SolutionObtain and expression for the work done by a torque.
View Solutionकिसी वस्तु द्वारा किये गये कार्य तथा किसी वस्तु पर किये गये कार्य में अंतर उदाहरण देकर समझाइए |
View SolutionExplain the work done by a varible force.
View SolutionIf τ is the torque and θ is the angular displacement then work done is given by
View SolutionCalculate the work done by the torque.
View SolutionIf τ is the torque and θ is the angular displacement then work done is given by
View SolutionCalculate the work done by the torque.
View SolutionThe work done by the torque is
View Solution
