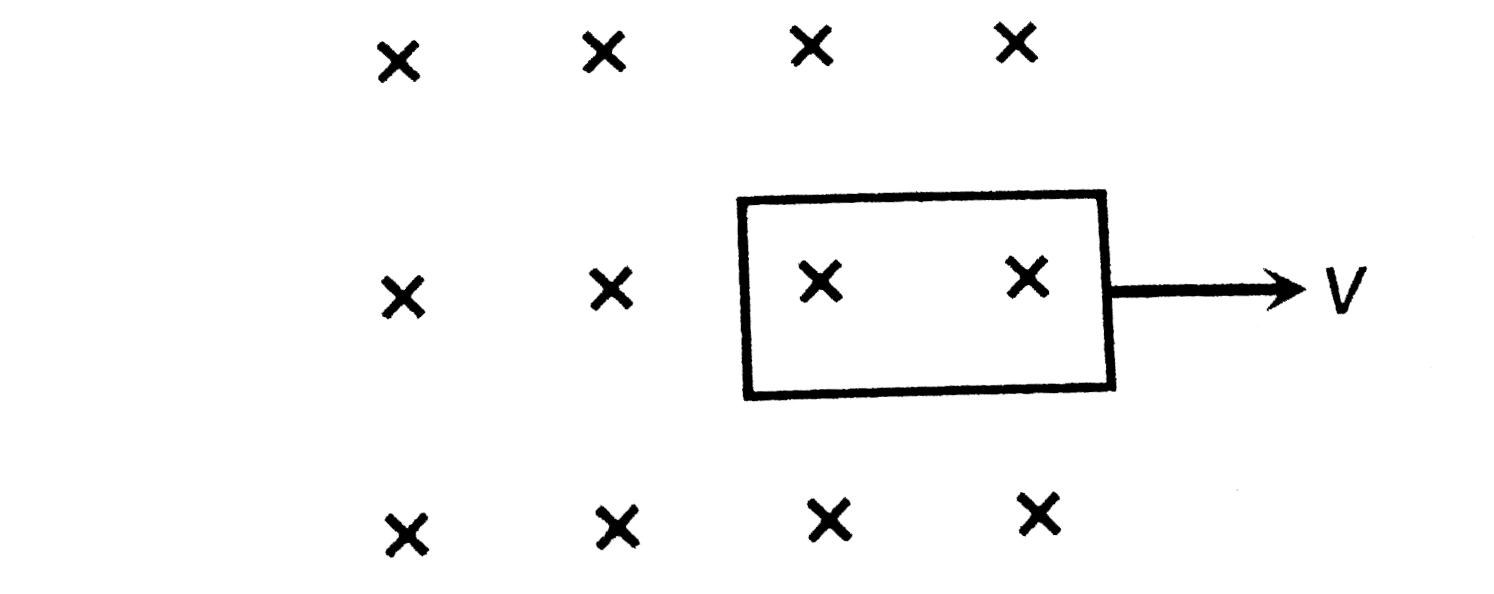
Figure show a square loop of side 0.5m and resistance 10Ω. The magnetic field has a magnitude B=1.0T. The work done in pulling the loop out of the field slowly and uniformly in 2.0s is
3.125×10−3J
6.25×10−4J
1.25×10−2J
5.0×10−4J
The correct Answer is:A
Speed of the loop should be
v=lt=0.52=0.25m/s
Induced emf, eBvl=(1.0)(1.0)(0.25)(0.5)
=0.125V
∴ Current in the loop i=eR=0.12510
=1.25×10−2A The magnetic force on the left arm due to the magnetic field is
Fm=ilB=(1.25×10−2(0.5)(1.0)
=6.25×10−3N
to pull the loop uniform an external force of 6.25×10−3N towards right must be applied.
∴W=(6.25×10−3N(0.5m)=3.125×10−3J
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B - Assertion Reasoning
31 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - AIPMTNEET Questions
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Applications Of Emi
58 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Figure shows a square loop 100 turns as area of 2.5×10−3m2 and a resistance of 100 Ω. The magnetic field has a magnitude B = 0.40 T . The work done in pulling the loop out of the field slowly and uniformly in 1.0s is n×10−6 then n is

View SolutionA conducting square loop of side 10 cm is placed in a region of uniform magnetic field 0.5 T as shown in the figure. Calculate the work done in slowly moving the loop out of the field in 2 seconds with a speed of 0.05ms−1. The resistance of loop is 10 Ω.

View Solution
Knowledge Check
Figures shows a square loop of side 1m and resistance 1Ω. The magnetic field on left side of line PQ has a magnitude B=1.0T. The work done in pulling the loop out of the field uniformly in 1 s is
 A1JB10JC0.1JD100J
A1JB10JC0.1JD100JFigure shows loop of 200 turns and side a=3m and resistance of one coil R=1000Ω. The work done in pulling the loop out of the field, slowly and uniformly in 1.0 s is
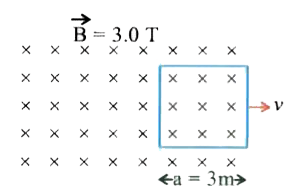 A130 JB125 JC146 JDNone
A130 JB125 JC146 JDNoneA circular loop of radius 0.0157 m carriesa current of 2.0 A. The magnetic field at the centre of the loop is
A1.57×10−5Wb/m2B8.0×10−6Wb/m2C2.5×10−5Wb/m2D3.14×10−5Wb/m2
Figure shows a square current carrying loop ABCD of side 2m and currenti=12A. The magnetic moment →M of the loop is

View SolutionA square loop of side 20 cm and resistance 0.30 Ω is placed in a magnetic field of 0.4 T. The magnetic field is at an angle of 45∘ to the plane of loop. If the magnetic field is reduced to zero in 0.5 s, then find the induced emf and induced current in the loop in this time interval.
View SolutionA square loop of side 20 cm is placed on a plane and magnetic field intensity of 0.1 T is applied at an angle 30 with the plane of the loop. Magnetic field is changed to zero uniformly within 0.8 second. Calculate the emf induced in the loop.
View SolutionA current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View SolutionA square loop of side 20 cm is placed on a plane and magnetic field intensity of 0.1 T is applied at an angle 30∘ with the plane of the loop. Magnetic field is changed to zero uniformly within 0.8 second. Calculate the induced emf and current in the loop.
View Solution
