figure show the identical simple pendulums of length. One is tilled at an angle α and imparted an initial velocity v1 towards mean position and at a velocity v2 at an initial angular displacement β. Find the phase difference in oscillations of these two pendulums

It is given that first pendulum bob is given a velocity v1 at a dislpacement lα from mean position , using the formula for velocity we can find the amplitude of its oscillation as
V1=ω√A21−(lα)2 [If A1, is the amplitude of SHM of this As for simple pendulum ω=√gl we have
V21=gl[(A21)−(lα)2)]
A1=√l2α2+v21lg (i)
Similarly if A2 is the amplitude of SHM of second pendlum bob we have
V2=ω√A21−(lβ)2
or A2=
⎷(l2β2+v22lg) (ii)
Now we repersent the two SHMs by circular motion representation as shown in figure
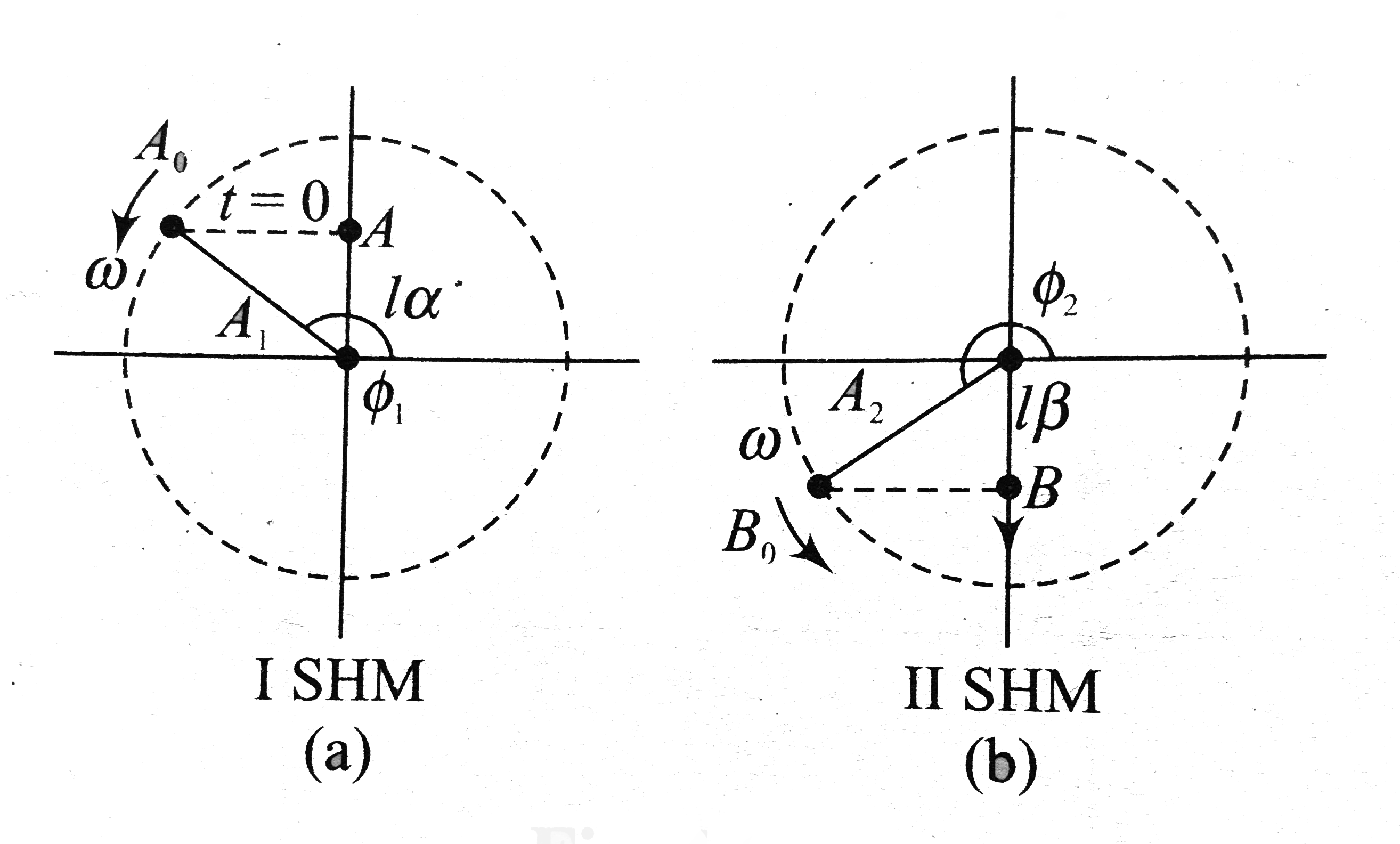
In first pendulum at t=0 the bob is thrown from a displacement lα from mean position with a velocity v1 towards mean position . As it is moving towards mean position in figure (a) , we consider the corresponding circular motion particle A0 of the bob A is second quarant, as the referance direction of ω we consider anticlockwise. As shown in figure initial phase of bob A is given as
ϕ1=π−sin−1(lαA1) (iii)
Similarly for second pendulum bob B, its corresponding circular motion partical B0att=0 is consider as shown in figure (b) its initial base is given as
ϕ2=sin−1(lβA2) (iv)
As both the pandulum are identical, their angular frequency for SHM must be same , so their phase difference can be given as
Δϕ=ϕ2−ϕ1sin−1(lβA2)+sin−1(lαA1)−π
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
figure show the identical simple pendulums of length. One is tilled at an angle α and imparted an initial velocity v1 towards mean position and at a velocity v2 at an initial angular displacement β. Find the phase difference in oscillations of these two pendulums

View SolutionTwo simple pendulum of unequal lengths wihile oscillating meet each other at mean position. What is their phase difference ?
View Solution
Knowledge Check
A pendulum is displaced to an angle θ from its equilibrium position, then it will pass through its mean position with a velocity v equal to
A√2glB√2glsinθC√2glcosθD√2gl(1−cosθ)Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
AL/3B3L/4C4L/3D5L/3A simple pendulum of Length l and mass (M) is oscillating in a plane about a vertical line between the angular limits −ϕto+ϕ. For an angular displacement θ(<|ϕ|), , the tension in the string T and velocity of the bob V are related as-
ATcosθ=MgBT = Mg cos θ+MV2/RCTangential acceleration is g sinθDT =Mg cos θ
Two simple pendulums of equal length cross each other at mean position. Then their phase difference is
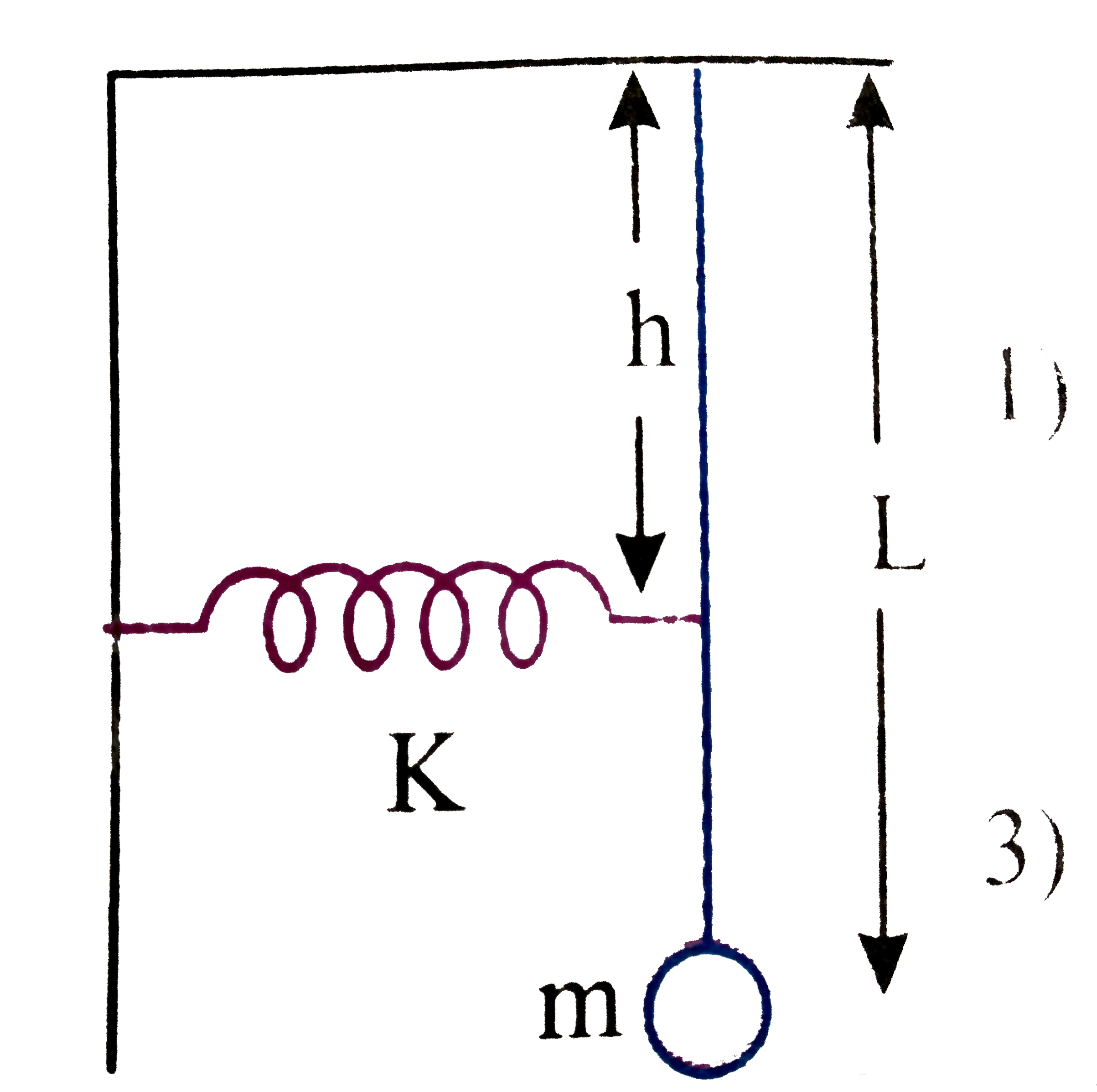
View SolutionA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
View SolutionA simple pendulum has a length l . What minimum velocity should be imparted to its bob at the mean position so that bob reaches a height equal to l above the point of suspension?
View SolutionAt any instant of time, the total energy (E) of a simple pendulum is equal to the sum of its kinetic energy (12mv2) and potential energy (12kx2) where, m is the mass, v is the velocity, x is the displacement of the bob and k is a constant for the pendulum, the amplitude of oscillation of the pendulum is 10 cm and its total energy is 4 m J. Find k.
View SolutionStatement-1 : During the oscillation so f a simple pendulum, the direction of its acceleration at the mean position is directed towards the point of suspension and at exteme position is direction towards the mean position .
Statement-2 : The directio of acceleration of a simple pendulum at an instant is decided by the tangential and radial components of weight at that instant.
View Solution
