Figure shown a charged conductor resting on an insulating stand. If at the point P the charge density is σ, the potential is V and the electric field strength is E, what are the values of these quantities at point Q ?

Charge densityPotentialElectric intensity>σ>V>E
Charge densityPotentialElectric intensity>σV>E
Charge densityPotentialElectric intensity<σVE
Charge densityPotentialElectric intensity<σV<E
The correct Answer is:D
The surface of the conductor is an equipotential surfaces since is free flow of electrons within the conductor. Thus potential at Q is the same as that at P. That is VP=VQ=V. The electric field E at a point on the equipotential surface of the conductor is inversely proportional to the square of theradius of curvature r at that point. that is E∝r−2
Since point Qhas a larger radius of curvature then that a point P, the electric field at Q is less than that at P.That is EQ<EP=E.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Euipotentials
45 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
An uncharged insulated conductor A is brought near a charged insulated condutor B. what happens to charge and potential of B ?
View SolutionThe figure shows three infinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area +σ,+2σ and −σ. Find the ratio of the net electric field at that point a to that at point B.
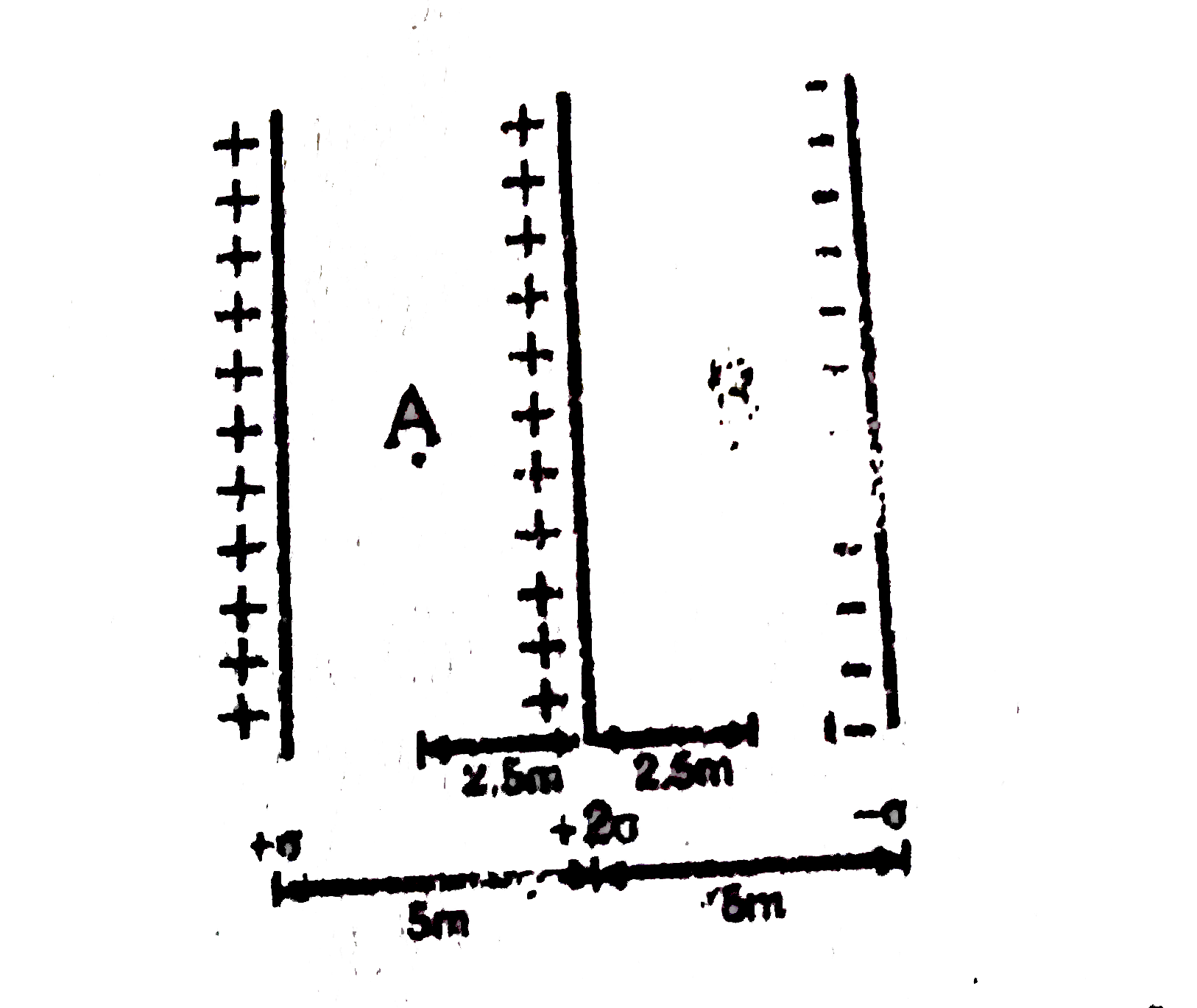
View Solution
Knowledge Check
A point P is at a distance r from a point charge q. if at point P, the electric potential is 300 V, and the electric field intensity is 75 V/m, then the distance of P from the point charge is
A2 mB4 mC8 mD10 mA conductor with a cavity is charged positively and its surface charge density is σ. If E and V represent the electric field and potential, then inside the cavity
AE = 0 and V = 0BE = 0 and σ- constantCV = 0 and σ = constantDE = 0 and V = constantA charged conductor of area ds is placed in electric field of strength E. The force acting on unit area of the conductor is
A∈0kE22B∈0k2ECE22∈0kD∈0kE2
The force exerted on a 3 C of charge placed at a point in an electric field is 9 N. Calculate the electric field strength at the point.
View SolutionThe electric intensity at a point near a charged conductor of surface charge density σ is
View SolutionTwo plane sheets of charge densities +σand−σ are kept in air as shown in Fig. What are electric field intensities at points A and B ?

View SolutionAt a certain distance from a point charge, the electric field is 500 V/m and the potential is 3000 V. What is the distance ?
View SolutionThree large parallel plates have unifrom surface charge densities as shown in the figure. What is the electric field at P
 .
.
View Solution
