Figure shows a cylindrical container containing oxygen gas and closed by a piston of mass 50kg. Piston can slide smoothly in the cylinder.Its crosssectional area is and atmospheric pressure is Pa. Someheat is supplied to the cylinder so that the piston is slowly displaced up by 20 cm. Find the amount ofheat supplied to the gas.

As here piston is open to atmosphere, the gas is under a constant pressure given as
Pa
Pa
It is given that the piston moves out by 20 cm, thus increment is its volume is given as
Thus in the process work done by gas is
[ As =constant ]
=300 J
For a process is which gas pressure is constant, work done can also be given as
or =300 J
As in the process gas pressure is constant thus heat supplied in raising the temperature by is given as
[As for as being diatomic gas ]
=1050 J
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Discussion Question
17 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct
21 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
Figure shows a cylindrical container containing oxyegn (γ=1.4) and closed by a 50 kg frictionless piston. The area of cross section is 100cm(2) , atmospheric pressure is 100kPa+E2 and g is 10 m s^(-2). The cylinder is slowly heated for some time. Find the amount of heat supplied to gas if the piston moves out through a distsnce of 20 cm.
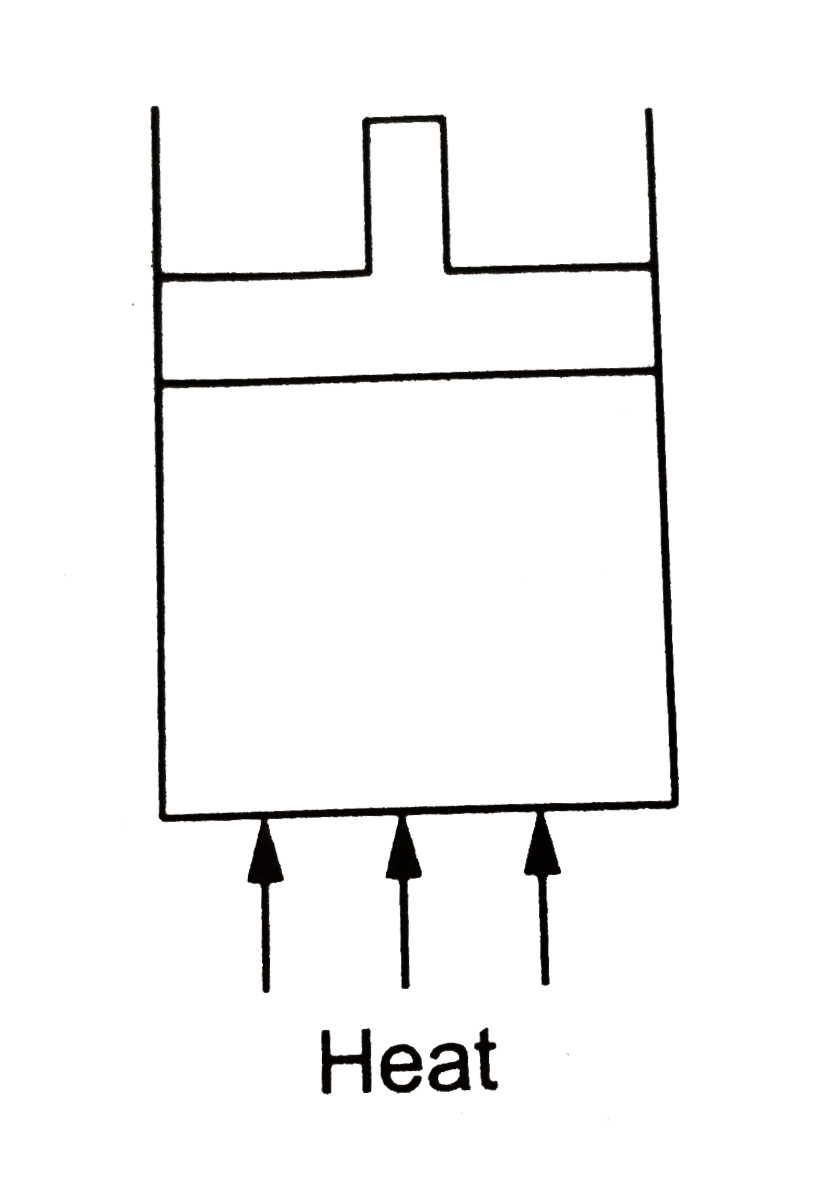 .
.
View SolutionFigure shows a cylindrical container containing oxyegn (γ=1.4) and closed by a 50 kg frictionless piston. The area of cross section is 100cm(2) , atmospheric pressure is 100kPa+E2 and g is 10 m s^(-2). The cylinder is slowly heated for some time. Find the amount of heat supplied to gas if the piston moves out through a distsnce of 20 cm.
 .
.
View Solution
Knowledge Check
An ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
Af=12π√γ(p0A2+MgA)V0MBf=12π√1γ(p0A2+MgA)V0MCf=12π√(p0A2+MgA)V0MDf=12π√A(p0A2+MgA)V0M
A cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
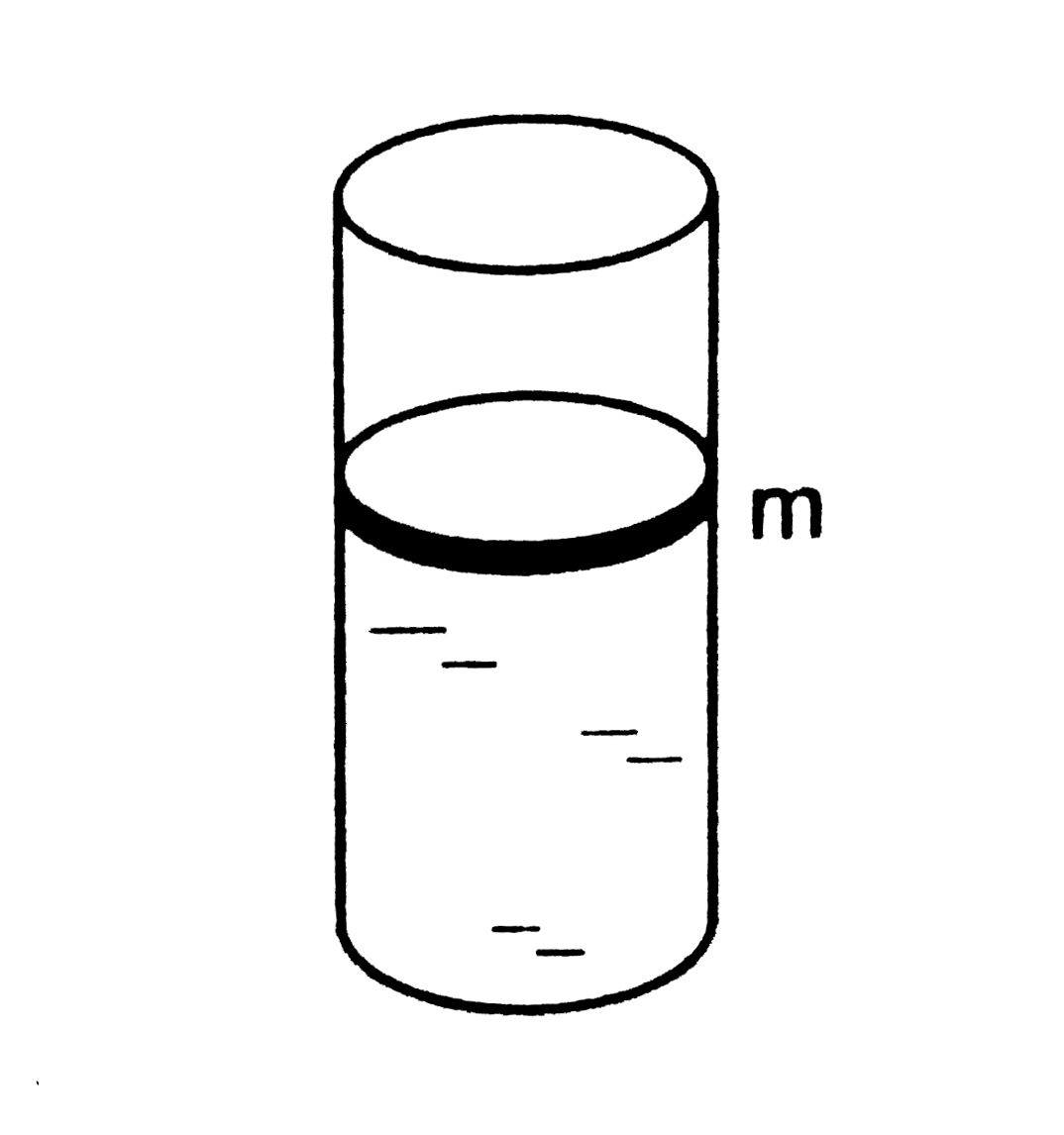 ,
,
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass "100g" as shown in the figure.The radius of the piston is "10cm" .If the atmospheric pressure is P0 then the pressure difference of the liquid just below the piston and the atmospheric pressure is (g=10ms2)
View SolutionFigure-2.47 shows a cylindrical container of radius 5cm and a piston is fitted in it to enclose a length of 20 cm in it.The cylinder contains an ideal gas at a pressure of 1 atmosphere and 300 K temperature.The cylinder is slowly heated and it is found that the piston starts displacing when the gas temperature reaches 600 K. It is given that the friction coefficient between the piston sidesand the container wall is 0.2. Find the normal force acting between piston sides and the container wall per unit length ofits circumference.
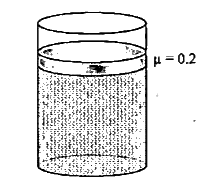
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionAn ideal gas is enclosed in a cylinder having cross sectional area A. The piston of mass M has its lower face inclined at θ to the horizontal. The lower face of the piston also has a hemispherical bulge of radius r. The atmospheric pressure is P0.
(a) Find pressure of the gas.
(b) The piston is slowly pulled up by a distance x. During the process the piston is always maintained in equilibrium by adding heat to the gas. [It means if the piston is left at any stage it will stay there in equilibrium]. Find change in temperature of the gas. Number of mole of the gas in the cylinder is one.
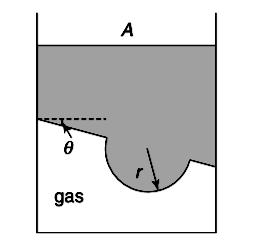
View Solution
