Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

(a) Consider the case r>a. The Amperian loop, labelled 2, is a circle concentric with the cross-section. For this loop, L=2πr
Ie=Current enclosed by the loop = I The result is the familiar expression for a long straight wire
B(2πr)=μ0I
B=μ0I2πr
B∝1r[r>α]
(b) Consider the case r<α, The Amperian loop is a circle labelled 1. For this loop, taking the radius of the circle to be r,
L=2πr
Now the current enclosed Ie is not I, but is less than this value. Since the current distribution is uniform, the current enclosed is, Ie=I(πr2πa2)=Ir2a2
Using Ampere's law, B(2πr)=μ0Ir2a2
B=(μ0I2πa2)r
B∝r(r<a)
B∝r(r<a)
Figure shows a plot of the magnitude of B with distance r from the centre of the wire. The direction of the field is tangential to the respective circular loop (1 or 2) and given by the right-hand rule described earlier in this section. This example possesses the required symmetry so that Ampere’s law can be applied readily.
Topper's Solved these Questions
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
A2:1B1:2C4:1D1:1 - Question 2 - Select One
A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1 - Question 3 - Select One
A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A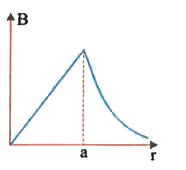 B
B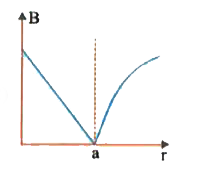 C
C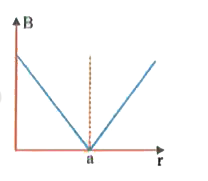 D
D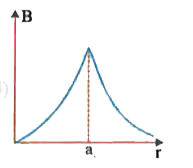
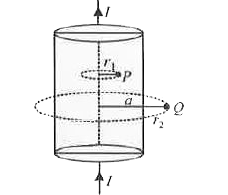
Figure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
 View Solution
View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
 View Solution
View SolutionWrite Ampere's circuital law.A long straight wire of a circular cross section (radius a) carrying steady current.Current is uniformly distributed in the wire.Calculate magnetic field inside the region (r<a) in the wire.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View Solution

