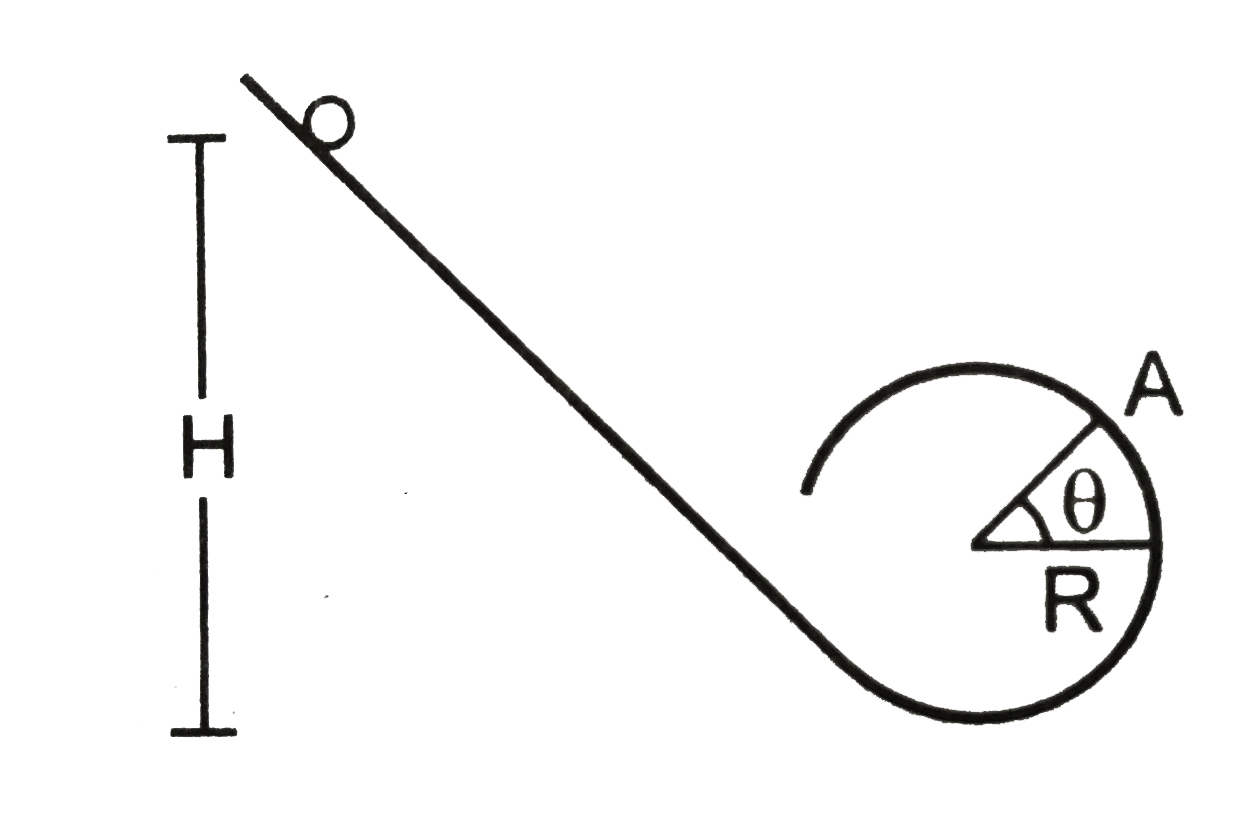
Figure shows a smasll sphereical bal of mass m rolling down the loop track. Thebasll is released on the linear portion at a verticla height H from the lowest point. The circular part show has a radius R.
a. find the kinetic energy of the ball when it is at a point where the radius makes an angle θ with the horizontal.
Find the radial and the tangential accelerations of the cente when the ball is at A. c. find the bnormal force and the frictionasl force acting on the ball if H=60 cm, R=10cm θ=0 and m=70 fg.
The correct Answer is:A, B, C, D
a. Total kinetic energy
y=12mv2+12Iω2
therefore, according to the question
mgH=12mv2+12Iω2+mgR(1+sinθ)
→mgH−mgR(1+sinθ)
=12mv2+12Iω2
→12mv2+12Iω2=mg(H−R−Rsinθ)
b. To find the acceleratiohn components,
→12mv2+12Iω2=mg(H−R−Rsinθ)
→k710mv2=mg(H−R−Rsinθ)
→v2=107g(H−R−Rsinθ)
→v2=107g(H−R−Rsinθ).....i
→v2R=107(g[H−R)−Rsinθ])R
→v2R=(10g[(H−R)−Rsinθ)])R
−2vdvdt=−(107)gRcosθdthηdt
→ωRdvdt=−(57)gRcosθdthηdt
→dvdt=−(57)gcosθ
→ tangential acceleration
c. Normal force at thea=0
mv2R=(70100)×(107)×10{(0.6−0.1)0.1}
=5N
Friction force:
=f=mg−ma
−f=m(g−a)
m(10−57x10)
=0.07(10−57×10)
=1100(70−50)=0.2N
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
A particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.View SolutionA ball leaves the track at B which is at 3m height from bottom most point of the track. The ball further rises upto 4m height from the bottom most point before falling down. Find h (in m), if the track at B makes an angle 30∘ with horizontal.
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.A2u2(1+cos2θ)3/2g2√2cosθBu2(1+cos2θ)3/2g2√2cosθCu2(1−sin2θ)3/2g2√2cosθDu2(1−tan2θ)3/2g2√2cosθ - Question 2 - Select One
A small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
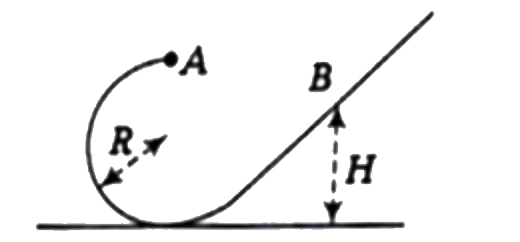 ARB2 RC3R2D5R2
ARB2 RC3R2D5R2
A uniform thin spherical shell of mass m and radius R rolls down without slipping over an inclined plane of angle θ with the horizontal. The ratio of rotational kinetic energy to the total kinetic energy of the shell will be
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
 View Solution
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
 View Solution
View SolutionInside a smooth spherical shell of the radius R a ball of the same mass is released from the shown position (Fig.) Find the distance travelled by the shell on the horizontal floor when the ball comes to the lowest point of the shell.
 View Solution
View SolutionFigure below shows a small mass connected to a string, which is attached to a vertical post. If the ball is released when the string is horizontal as shown, the magnitude of the total acceleration (including radial and tangential) of the mass as a function of the angle Θis
 View Solution
View SolutionA small sphereical ball is released from a point at a height h on a rough track shown in figure. Assuming that it dow not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
 View Solution
View Solution

