Figure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was M. With what gravitational force does the hollowed out lead sphere attract a particle of mass m that lies at a distance d from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
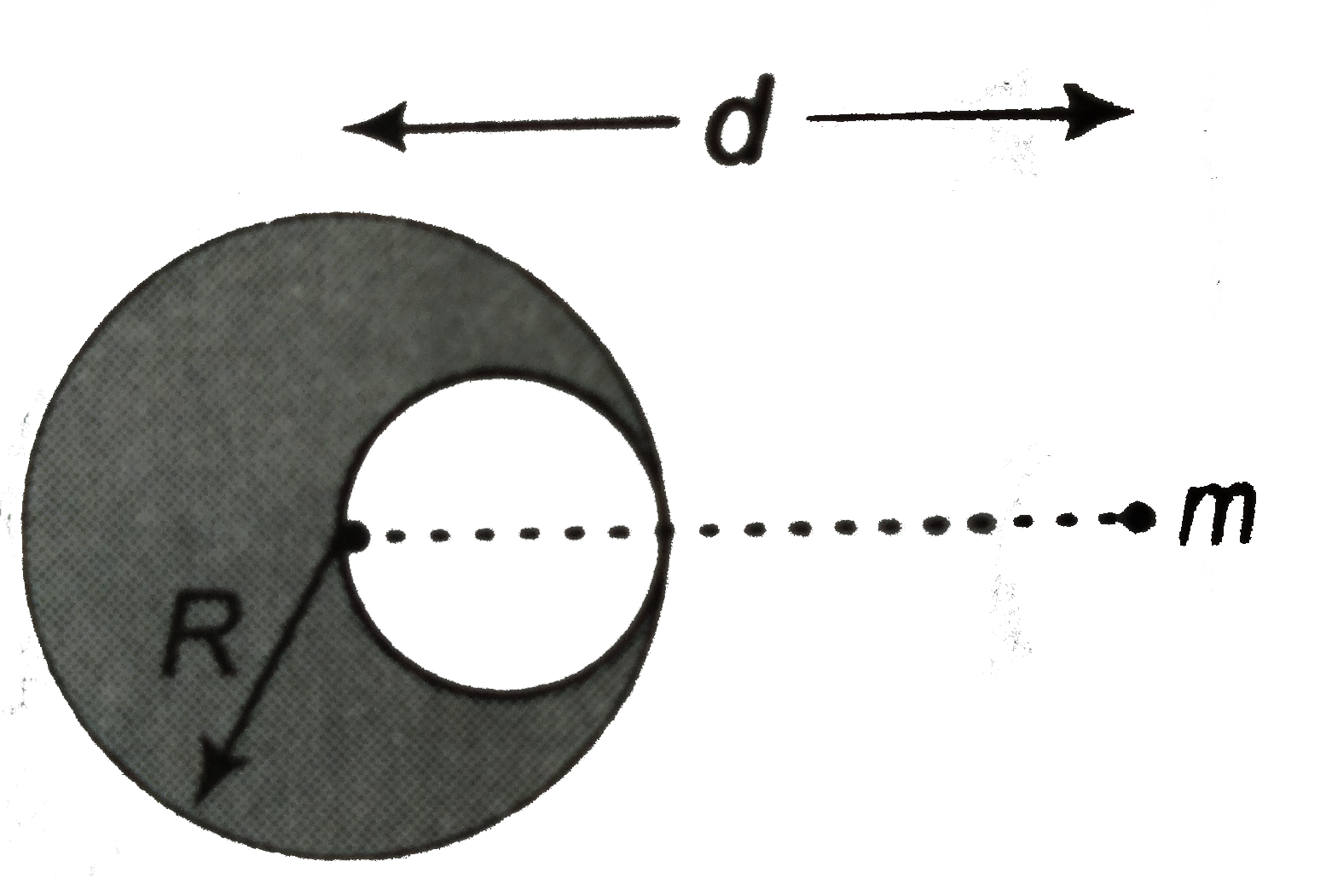
Let O be the centre of the solid sphere and O' that of the hollow. For an external point the sphere behaves as if is entire mass is concentrated at its centre. Therefore, the gravitatioinal foorce on a mass m at P due to the original sphere (of mass M) is
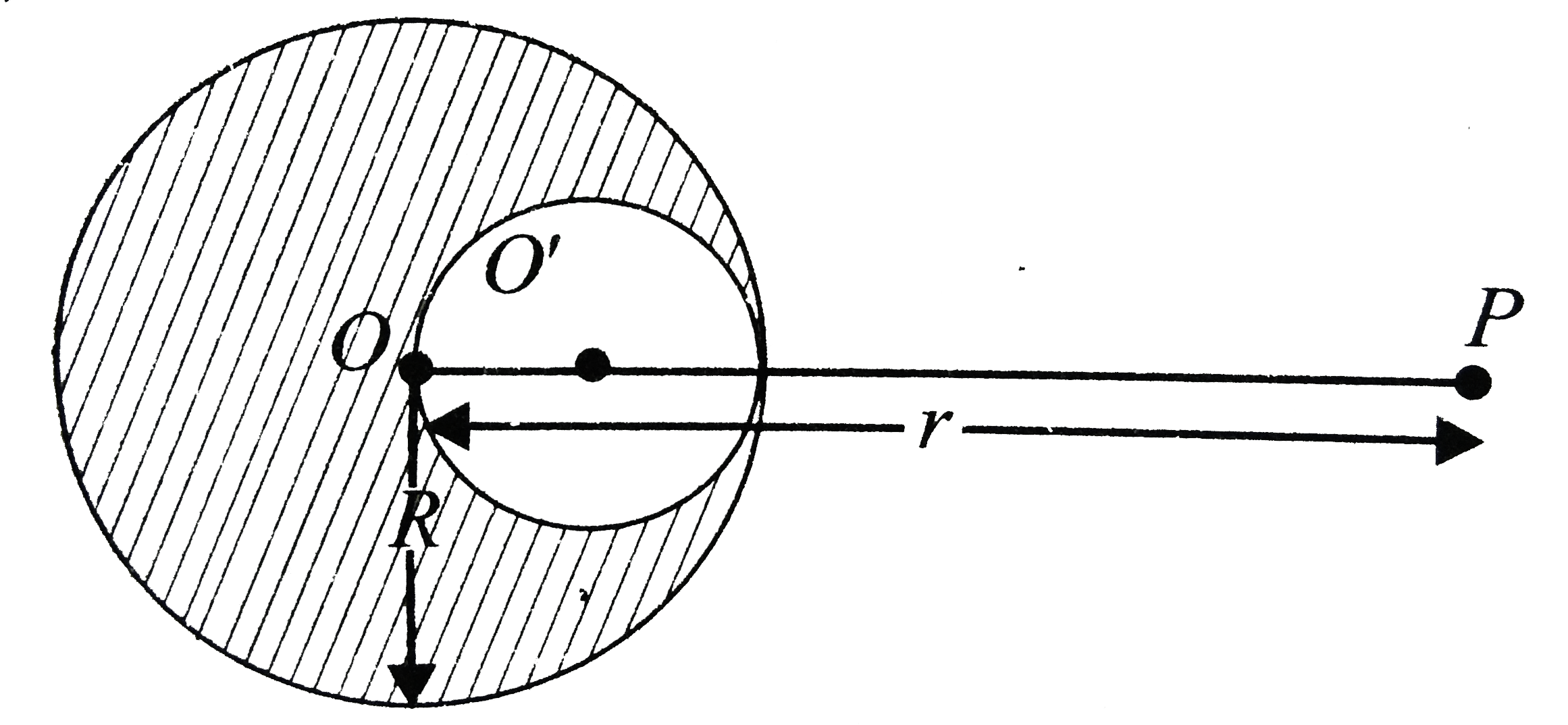
F=GMmr2, along PO
The diameter of the smaller sphere (which would be cut of) is R, so that its radius OO' is R/2. The force on m at P due to this sphere of mass M (say) would be
F'=GM'm(r−R2)2 along PO' (∵ distance PO'=r−R/2)
As the radius of this sphere is half of that of the original sphere, we have
M'=m8
Therefoe F'=GMm8(r−R/2)2 along PO'
As both F and F' point along the same direction, the force due to the hollowed sphere is
F−F′=GMmr2−GMm8r2(1−R(2r)2)
=GMmr2⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩1−18(1−R(2R)2)⎫⎪
⎪
⎪
⎪⎬⎪
⎪
⎪
⎪⎭
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.113videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.215videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
A spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is
 View Solution
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
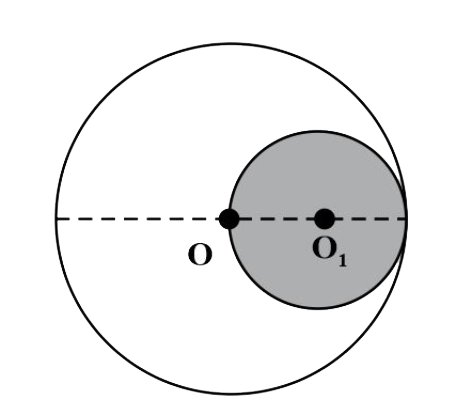
View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
 View Solution
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
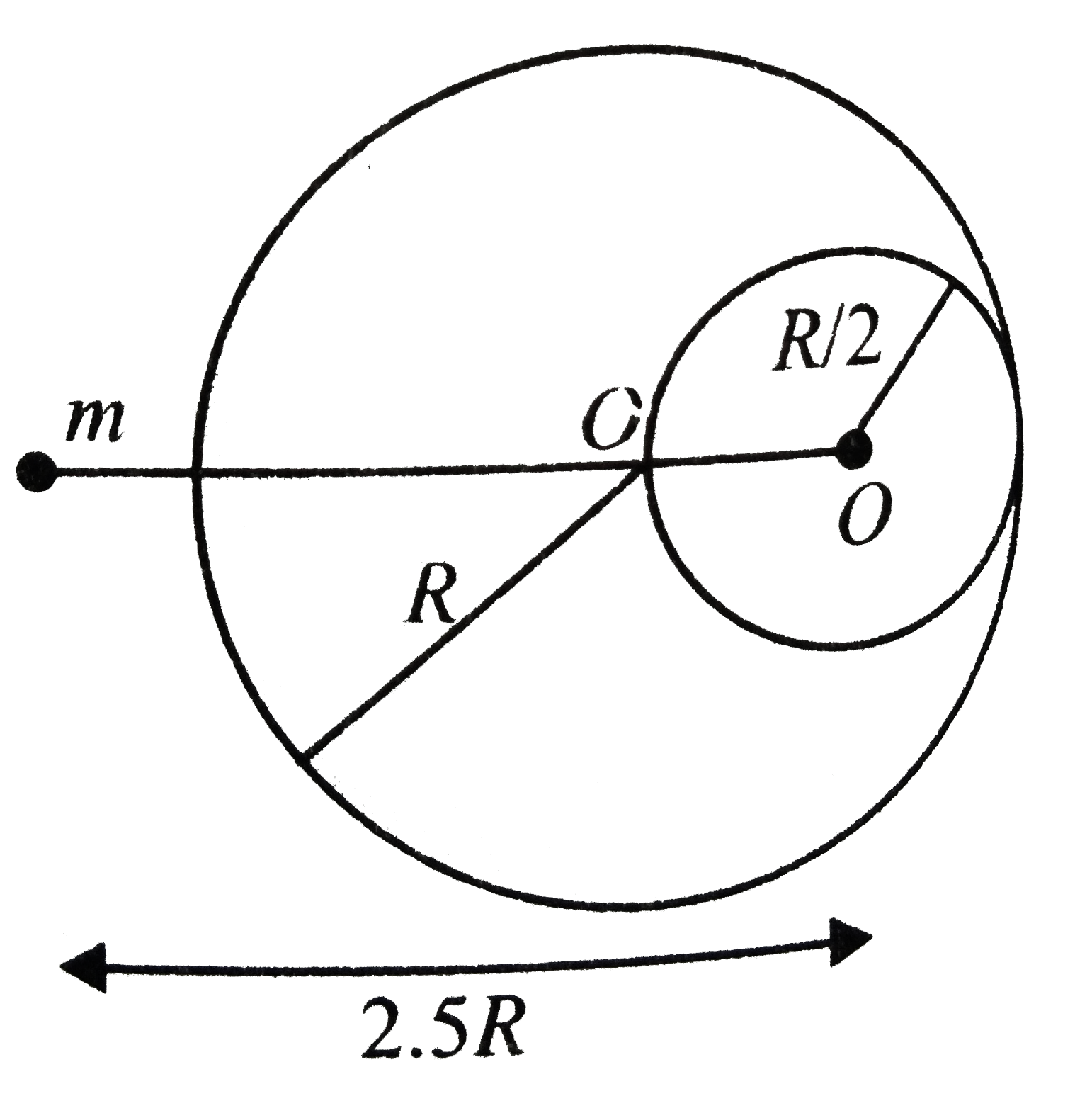 View Solution
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
 View Solution
View SolutionTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View Solution

