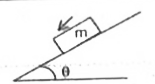
Figure shows a spring fixed at the bottom end of an incline of inclination 370. A small block of mass 2 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find a. the frictioin coefficient between the plane and the block and b. the spring constant of the spring. Take g=10ms2.
The correct Answer is:A, B
m=2kg,S1=4.8m,x=20cm=0.2m
S2=1m
sin370=0.60=35
θ=370
cos 37^0=0.80=4/5=10m/sec^2<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_080_S01.pngwh=80%sty≤=background:white;><br>Apply∈gworke≠rgypr∈cip≤fordownwardmotionofthebody<br>0-0=mgsin37^0(x+4.8)-muRx5-1/2kx62<br>20xx(0.80)xx5-1/2k(0.2)^2=0<br>rarr 60-80mu-0.02k=0<br>→80mu+0.02k=60<br>Similarlyfortheupwardmotionofthebodytheequationis<br>0-0=(-mgsin37^0)-muRx1+1/(2k)(-2)^2<br>rarr 20xx(0.06)xx1-muxx20xx(0.80)xx1-1/2k(0.2)^2<br>rarr 12-16mu+0.02k=0<br>Adding equation i and equation ii we get
96μ=48
→μ=0.5
Now putting the value of μ in equation i,
k=1000Nm
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
Knowledge Check
- Question 1 - Select One
A block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ⟨h and spring constant = K)-
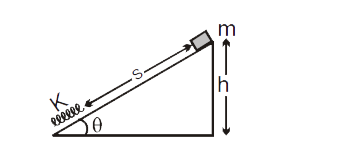 A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh/mK)1/2
A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh/mK)1/2 - Question 2 - Select One
block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ltlth and spring constant = K) - (A) (2mgh/K)1/2
 A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh//mK)^(1//2)
A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh//mK)^(1//2) - Question 3 - Select One
ϕ is the angle of the incline when a block of mass m just starts slipping down. The distance covered by the block if thrown up the incline with an initial speed v0 is :
Av204gsinϕB4v20gsinϕCv20sinϕ4gD4v20sinϕg
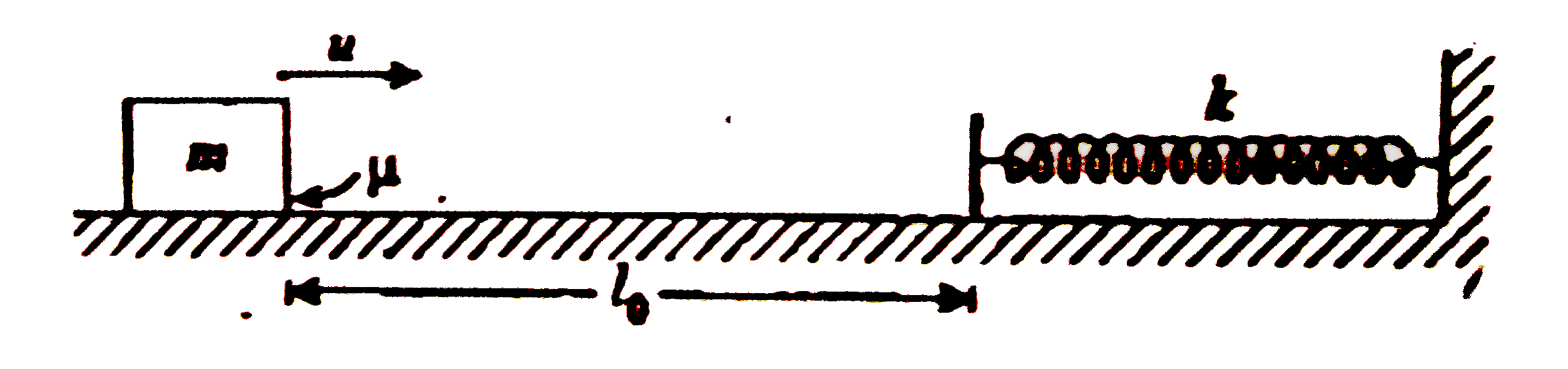
Figure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
 View Solution
View SolutionFigure shown two blocks in contact sliding down an inclined surface of inclination 30∘. The block of mass 2kgand the incline is μ1=0.20 and the incline is μ2=0.30 .Find the acceleration of 2.0kg block (in ms−2)g=10ms−2
 View Solution
View Solutionϕ is the angle of the incline when a block of mass m just starts slipping down. The distance covered by the block if thrown up the incline with an initial speed v0 is :
View SolutionFigure. shows a rough incline at an angle θ with coefficient of friction μ At the bottom a spring is attached with force constant k. A block of mass m is released from a position at a length l away from the spring. Write down the work energy equations to find the maximum compression in the spring and the distance by which the block rebound up the inclined plane. the distance by which the block rebound up the inclined plane
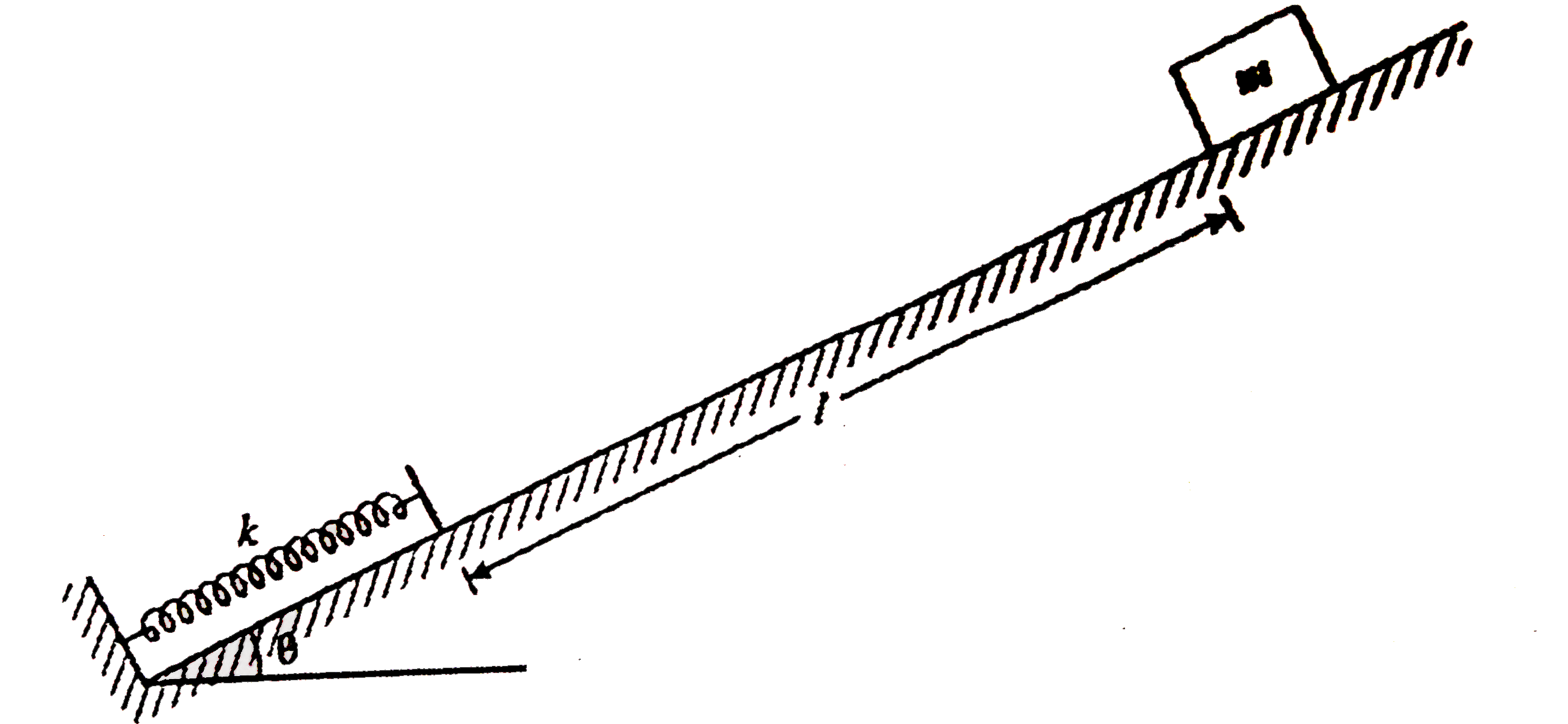 View Solution
View SolutionA block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
View Solution