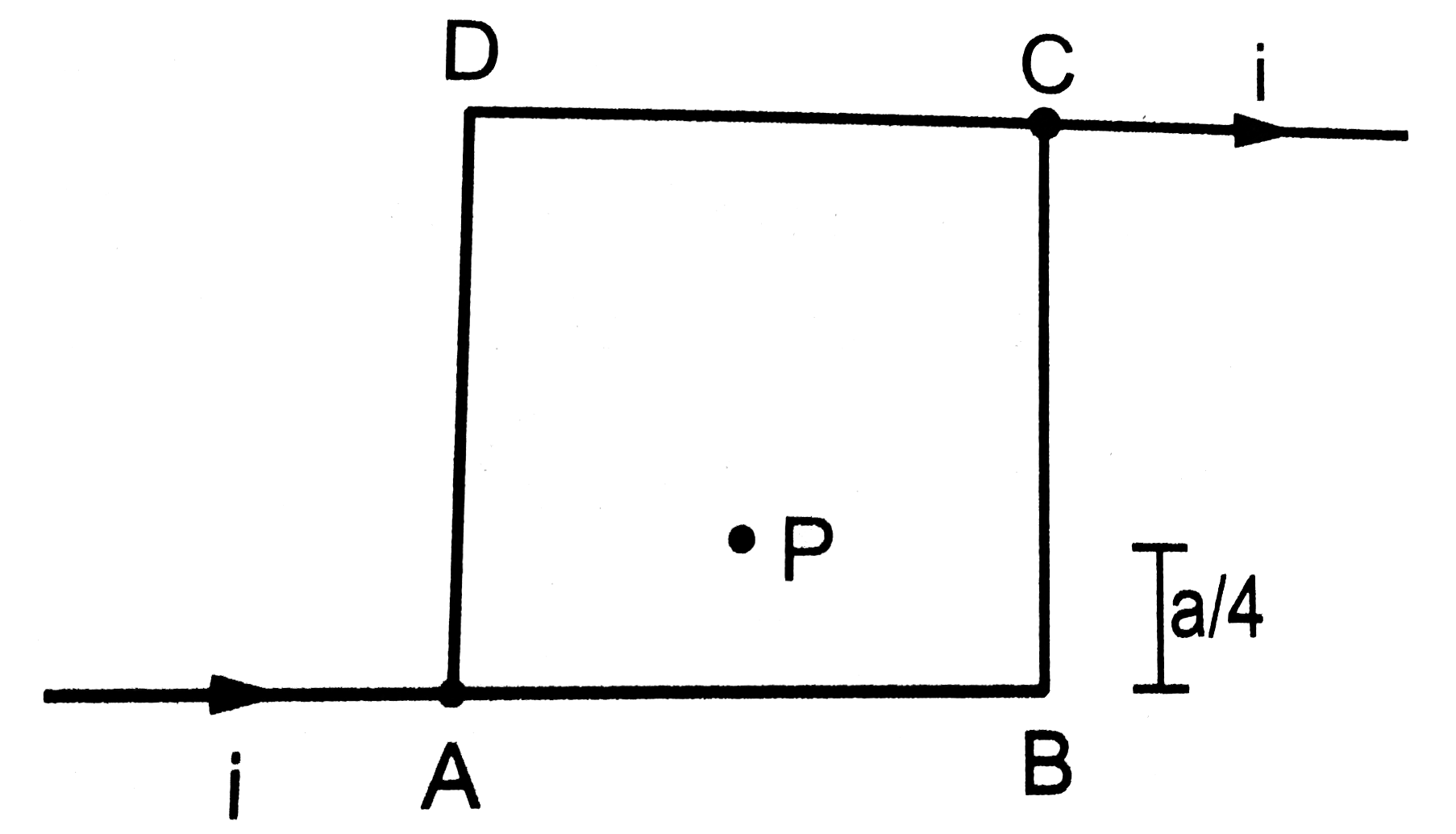
Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
 Solution in Gujrati
Solution in Gujrati
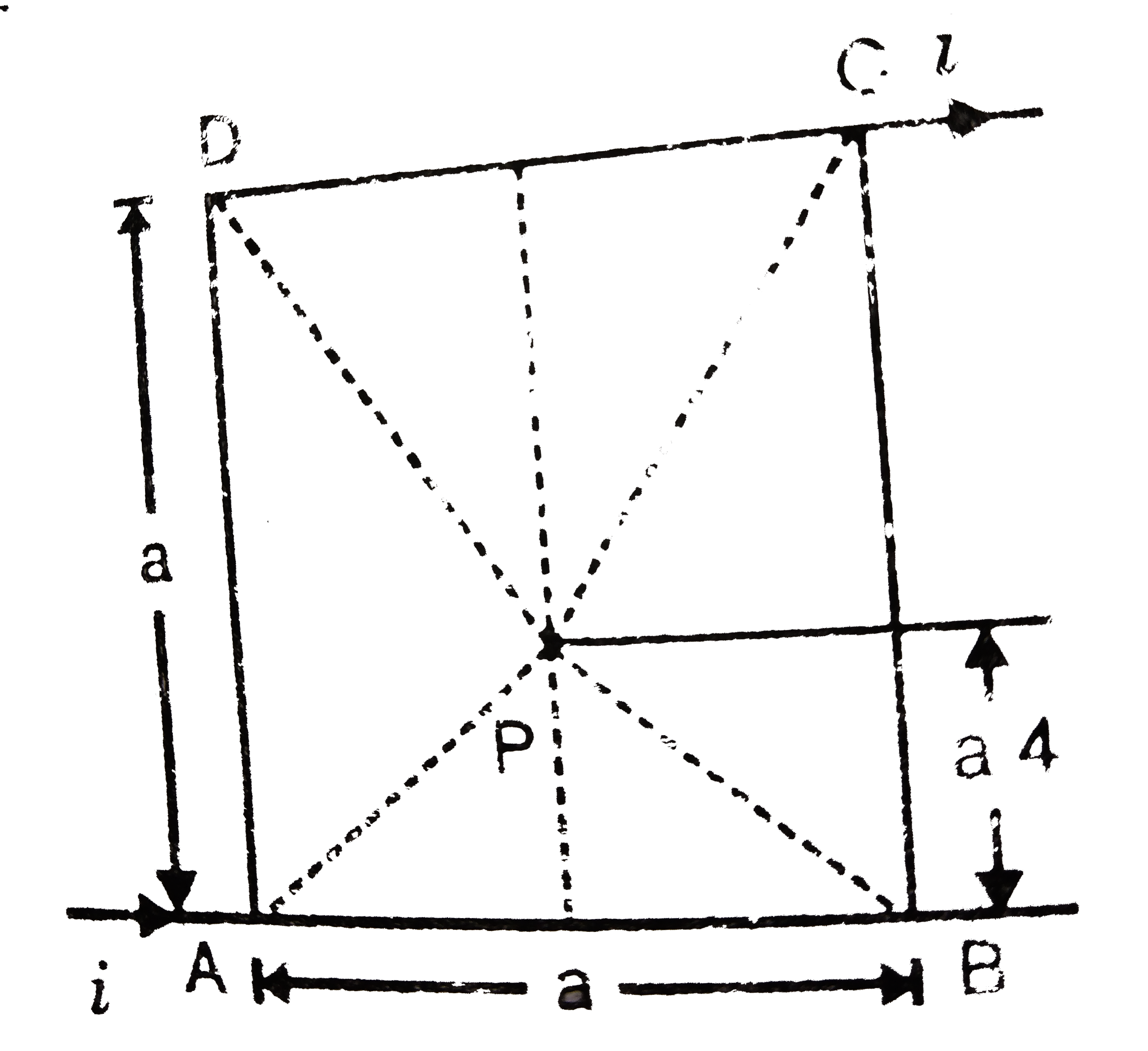
B at P due to AD =μo4π.i2.4a2.a⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦along
=μoi2πa⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦ along<br>BatPdue→AC=(mu_o)/(4pi).(i)/(2). (16)/(9a^2.a 2.[(((3a)/(4)))/(sqrt(((3a)/(4))^2 + ((a)/(2))^2))<br>(4mu_oi)/(9pia) [(((3a)/(4)))/(sqrt(((a)/(4))^2 +((3a)/(2))^2))]along<br>B at P due to AB = (mu_oi)/(4pi).(i)/(2) . (16)/(9a^2). a. 2 [(((a)/(4)))/sqrt(((a)/(4))^2 + ((a)/(2))^2 along<br>BatPdue→BC = (mu_o)/(4pi).(i)/(2). (4)/(a^2).a. [(((a)/(2)))/ sqrt(((a)/(2))^2 + ((a)/(2))^2) +(((a)/(2)))/sqrt(((a)/(2))^2 + ((3a)/(4))^2)] along<br>=(um_oi)/(2pia)[(((a)/(2)))/sqrt(((a)/(2))^2 +((a)/(2))^2) + (((a)/(2)))/(sqrt(((a)/(2))^2 +((3a)/(4))^2))]along⊗<br>so,net B=4μoiπa⎡⎢
⎢
⎢
⎢⎣(a4)√(a2)2+(a4)2⎤⎥
⎥
⎥
⎥⎦−4μoi9πa⎡⎢
⎢
⎢
⎢⎣(3a4)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦
=4μoiπa.14⎡⎢
⎢⎣1√14+116−4μoi9πa.34⎡⎢
⎢⎣1√14+916⎤⎥
⎥⎦
=4μoiπa[4√5]−μoi3πa[4√13][4√13]along
=4μoi2πa[1√5−13√13]along=2πoiπa[1√5−13√13]along.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
The magnetic field at the origin due to a current element I (→dl) placed at a positon (→r) is
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.

View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View SolutionFigure shows a square loop made from a uniform wire. Find the magnetic field at the centre of the square if a battary is connected between points A and C.

View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionThere is one circular loop of a uniform wire whose radius is R. Electric current I enters at one point on its circumference and leaves at a diametrically opposite point. What will be the net magnetic field intensity at the centre of the loop?
View SolutionThere is a circular loop of current of radius , as shown in figure: If current enters at point A and leaves at point B where angle AOB " is " 90^(@) and the wire of the loop is of uniform cross section area, then calculate the magnetic field intensity at the centre of the loop.
View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D . The magnetic field is :

View SolutionPQRS समरूप चालक तार से बना हुआ एक वर्गाकार लूप है। चित्रानुसार बिन्दु P पर धारा प्रवेश करती है तथा O से बाहर निकलती है। तब चुम्बकीय क्षेत्र होगा

View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View SolutionABCD is a square loop made of an uniform conducting wire. The current enters the loop at A and leaves at D. The magnetic field is
View Solution
